
【题目】![]() 是等边三角形,
是等边三角形,![]() 为平面内的一个动点,
为平面内的一个动点,![]() ,
,![]() 平分
平分![]() ,且
,且![]() .
.
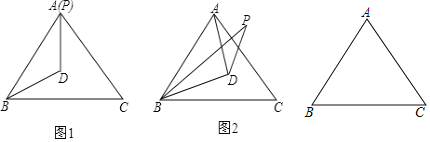
(1)当![]() 与
与![]() 重合时(如图1),求
重合时(如图1),求![]() 的度数;
的度数;
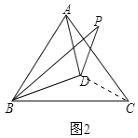
(2)当![]() 在
在![]() 的内部时(如图2),求
的内部时(如图2),求![]() 的度数;
的度数;
(3)当![]() 在
在![]() 的外部时,请你直接写出
的外部时,请你直接写出![]() 的度数为 .
的度数为 .
【答案】(1)![]() ;(2)
;(2)![]() ;(3)30°或150°
;(3)30°或150°
【解析】
(1)由于P,A重合,DP=DB,∠DBP=∠BPD,因为DB是∠PBC的平分线,可得∠DBP=∠BPD=30°;
(2)连接CD,由“SAS”可证△PBD≌△CBD,可得∠BPD=∠BCD,由“SSS”可证△BCD≌△ACD,可得∠BCD=∠ACD=![]() ∠ACB=30°,即可求解;
∠ACB=30°,即可求解;
(3)分三种情况:①当BP在AB的左侧,BD在△ABC内部时;②当BP,BD都在三角形外部,且∠BPD为锐角时;③当BP,BD都在△ABC外部,且∠BPD为钝角时,同(2)中的步骤分别求解.连接CD,步骤有2个,一是证明△PBD≌△CBD,从而得出∠BPD=∠BCD,二是证明△BCD≌△ACD,得出∠BCD=∠ACD,从而可得出结果.
解:(1)∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ;
;
(2)连接![]() ,
,
∵点![]() 在
在![]() 的平分线上,
的平分线上,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
在![]() 和
和![]() 中,
中,
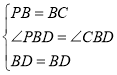 ,
,
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)如图3,连接CD,
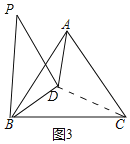
同(2)可得△ACD≌△BCD(SSS),
∴∠ACD=∠BCD=30°,
同(2)可得△PBD≌△CBD(SAS),
∴∠BPD=∠BCD=30°;
如图4,连接CD,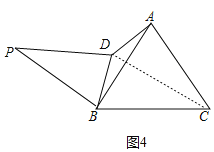
同理可得△ACD≌△BCD(SSS),
∴∠ACD=∠BCD=30°,
同理可得△PBD≌△CBD(SAS),
∴∠BPD=∠BCD=30°;
如图5,连接CD,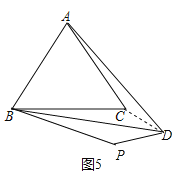
同理可得△ACD≌△BCD(SSS),
∴∠ACD=∠BCD=(360°-60°)÷2=150°,
同理可得△PBD≌△CBD(SAS)
∴∠BPD=∠BCD=150°.
综上可知,∠BPD的度数为30°或150°,
故答案为:30°或150°.


科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的
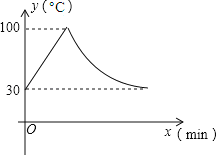
A.7:20 B.7:30 C.7:45 D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
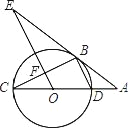
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AE于点E.
(1)求证:△BEF∽△DBC.
(2)若⊙O的半径为3,∠C=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书店老板去图书批发市场购买某种图书,第一次用 1200 元购买若干本,按 每本 10 元出售,很快售完.第二次购买时,每本书的进价比第一次提高了 20%,他用1500 元所购买的数量比第一次多 10 本.
(1)求第一次购买的图书,每本进价多少元?
(2)第二次购买的图书,按每本 10 元售出 200 本时,出现滞销,剩下的图书降价后全部 售出,要使这两次销售的总利润不低于 2100 元,每本至多降价多少元?(利润=销售收入一进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .按照以下步骤作图:①以点
.按照以下步骤作图:①以点![]() 为圆心,以适当的长为半径作弧,分别交
为圆心,以适当的长为半径作弧,分别交![]() 的两边于
的两边于![]() 两点,连接
两点,连接![]() .②分别以点
.②分别以点![]() 为圆心,以大于线段
为圆心,以大于线段![]() 的长为半径作弧,两弧在
的长为半径作弧,两弧在![]() 内交于点
内交于点![]() ,连接
,连接![]() .③连接
.③连接![]() 交
交![]() 于点
于点![]() .下列结论中错误的是( )
.下列结论中错误的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,四边形
的直径,四边形![]() 是内接正方形.
是内接正方形.
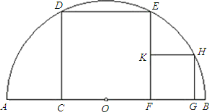
(1)求证:![]() ;
;
(2)在正方形![]() 的右侧有一正方形
的右侧有一正方形![]() ,点
,点![]() 在
在![]() 上,
上,![]() 在半圆上,
在半圆上,![]() 在
在![]() 上.若正方形
上.若正方形![]() 的边为
的边为![]() ,求正方形
,求正方形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“两免一补”政策,某市2011年投入教育经费2500万元,预计2013年要投入教育经费3600万元,已知2011年至2013年的教育经费投入以相同的百分率逐年增长,则2014年要投入的教育经费为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com