
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,连接
,连接![]() ,
,![]() .动点
.动点![]() 在
在![]() 上从点
上从点![]() 向终点
向终点![]() 匀速运动,同时,动点
匀速运动,同时,动点![]() 在射线
在射线![]() .上从点
.上从点![]() 沿
沿![]() 方向匀速运动,当点
方向匀速运动,当点![]() 运动到EF的中点时,点
运动到EF的中点时,点![]() 恰好与点
恰好与点![]() 重合,点
重合,点![]() 到达终点时,
到达终点时,![]() ,
, ![]() 同时停止运动.
同时停止运动.
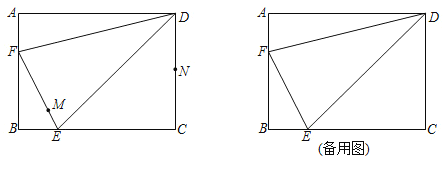
(1)求![]() 的长.
的长.
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并写出自变
的函数表达式,并写出自变![]() 的取值范围.
的取值范围.
(3)连接![]() ,当
,当![]() 与
与![]() 的一边平行时,求
的一边平行时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() );(3)
);(3)![]() 的值为
的值为![]() 或12
或12
【解析】
(1)由矩形的性质可得:∠B=90°,在Rt△BEF中,根据勾股定理即可求出EF的长;
(2)已知![]() ,
,![]() ,根据“当点
,根据“当点![]() 运动到EF的中点时,点
运动到EF的中点时,点![]() 恰好与点
恰好与点![]() 重合”,即可求出
重合”,即可求出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
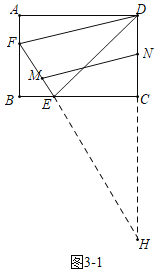
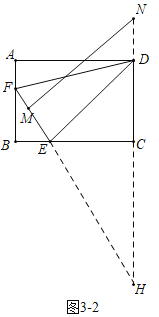
(3)如图3-1和3-2中,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,根据相似三角形的判定定理可证得
,根据相似三角形的判定定理可证得![]() ,根据相似三角形对应边成比例可得EH,CH的长,然后分三种情况讨论:①
,根据相似三角形对应边成比例可得EH,CH的长,然后分三种情况讨论:①![]() ,②
,②![]() ,③
,③![]() ,排除掉不存在的情况,继而根据相似三角形对应边成比例即可求解.
,排除掉不存在的情况,继而根据相似三角形对应边成比例即可求解.
(1)∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由题意得: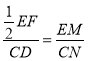 ,
,
即![]() .
.
∴![]() (
(![]() ).
).
(3)如图,延长![]() 交
交![]() 的延长线于
的延长线于![]() .
.
∵四边形ABCD是矩形,
∴∠B=∠ECD=∠ECH=90°,
又∵∠BEF=∠CEH,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
①如图3-1,当![]() 时,△HMN∽△HFD,
时,△HMN∽△HFD,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
②当![]() 时,这种情形不存在.
时,这种情形不存在.
③如图3-2中,当![]() 时,△HED∽△HMN,
时,△HED∽△HMN,
∴![]() ,即
,即![]() ,
,
∵![]() ,解得
,解得![]() ,
,
综上所述,满足条件的![]() 的值为
的值为![]() 或12.
或12.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
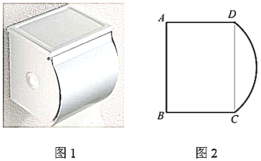
【题目】如图1是一种纸巾盒,由盒身和圆弧盖组成,通过圆弧盖的旋转来开关纸巾盒.如图2是其侧面简化示意图,已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,圆弧盖板侧面
,圆弧盖板侧面![]() 所在圆的圆心
所在圆的圆心![]() 是矩形
是矩形![]() 的中心,绕点
的中心,绕点![]() 旋转开关(所有结果保留小数点后一位).
旋转开关(所有结果保留小数点后一位).
(1)求![]() 所在
所在![]() 的半径长及
的半径长及![]() 所对的圆心角度数;
所对的圆心角度数;
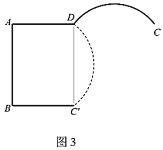
(2)如图3,当圆弧盖板侧面![]() 从起始位置
从起始位置![]() 绕点
绕点![]() 旋转
旋转![]() 时,求
时,求![]() 在这个旋转过程中扫过的的面积.
在这个旋转过程中扫过的的面积.
参考数据:![]() ,
,![]() ,
,![]() 取3.14.
取3.14.
查看答案和解析>>
科目:初中数学 来源: 题型:
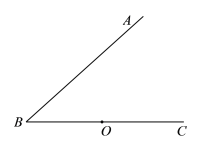
【题目】如图,点O为∠ABC的边![]() 上的一点,过点O作OM⊥AB于点
上的一点,过点O作OM⊥AB于点![]() ,到点
,到点![]() 的距离等于线段OM的长的所有点组成图形
的距离等于线段OM的长的所有点组成图形![]() .图形W与射线
.图形W与射线![]() 交于E,F两点(点在点F的左侧).
交于E,F两点(点在点F的左侧).
(1)过点![]() 作
作![]() 于点
于点![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的长;
,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠![]()
![]() ,判断射线BD与图形
,判断射线BD与图形![]() 公共点的个数,并证明.
公共点的个数,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x+4的图象与反比例函数y2=![]() 的图象交于A(﹣1,a),B两点,与x轴交于点C.
的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求k.
(2)根据图象直接写出y1>y2时,x的取值范围.
(3)若反比例函数y2=![]() 与一次函数y1=x+4的图象总有交点,求k的取值.
与一次函数y1=x+4的图象总有交点,求k的取值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=( )
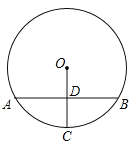
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
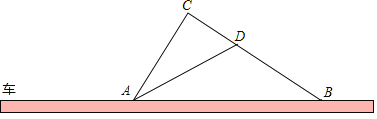
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com