
【题目】在平面直角坐标系![]() 中,对“隔离直线”给出如下定义:点
中,对“隔离直线”给出如下定义:点![]() 是图形
是图形![]() 上的任意一点,点
上的任意一点,点![]() 是图形
是图形![]() 上的任意一点,若存在直线
上的任意一点,若存在直线![]() :
:![]() 满足
满足![]() 且
且![]() ,则称直线
,则称直线![]() :
:![]() 是图形
是图形![]() 与
与![]() 的“隔离直线”,如图
的“隔离直线”,如图![]() ,直线
,直线![]() :
:![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的一条“隔离直线”.
的一条“隔离直线”.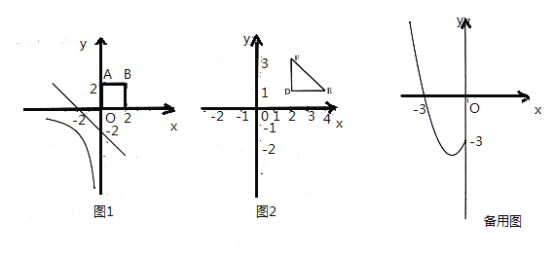
(1)在直线①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,是图
中,是图![]() 函数
函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”的为 .
的“隔离直线”的为 .
(2)如图![]() ,第一象限的等腰直角三角形
,第一象限的等腰直角三角形![]() 的两腰分别与坐标轴平行,直角顶点
的两腰分别与坐标轴平行,直角顶点![]() 的坐标是
的坐标是![]() ,⊙O的半径为
,⊙O的半径为![]() ,是否存在
,是否存在![]() 与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
与⊙O的“隔离直线”?若存在,求出此“隔离直线”的表达式:若不存在,请说明理由;
(3)正方形![]() 的一边在
的一边在![]() 轴上,其它三边都在
轴上,其它三边都在![]() 轴的左侧,点
轴的左侧,点![]() 是此正方形的中心,若存在直线
是此正方形的中心,若存在直线![]() 是函数
是函数![]() 的图像与正方形
的图像与正方形![]() 的“隔离直线”,请直接写出
的“隔离直线”,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①④;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据的“隔离直线”的定义即可解决问题;
(2)存在,连接![]() ,求得
,求得![]() 与
与![]() 垂直且过
垂直且过![]() 的直接就是“隔离直线”,据此即可求解;
的直接就是“隔离直线”,据此即可求解;
(3)分两种情形正方形在x轴上方以及在x轴下方时,分别求出正方形的一个顶点在直线![]() 上时的t的值即可解决问题.
上时的t的值即可解决问题.
(1)根据的“隔离直线”的定义可知![]() ,是图1函数
,是图1函数![]() 的图象与正方形OABC的“隔离直线”;直线
的图象与正方形OABC的“隔离直线”;直线![]() 也是图1函数
也是图1函数![]() 的图象与正方形OABC的“隔离直线”;而
的图象与正方形OABC的“隔离直线”;而![]() 与
与![]() 不满足图1函数
不满足图1函数![]() 的图象与正方形OABC的“隔离直线”的条件;
的图象与正方形OABC的“隔离直线”的条件;
故答案为:①④;
(2)存在,
理由如下:
连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,如图,
,如图,
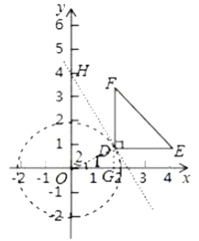
在Rt△DGO中,![]() ,
,
∵⊙O的半径为![]() ,
,
∴点D在⊙O上.
过点D作DH⊥OD交y轴于点H,
∴直线DH是⊙O的切线,也是△EDF与⊙O的“隔离直线”.
设直线OD的解析式为![]() ,
,
将点D(2,1)的坐标代入得![]() ,
,
解得:![]() ,
,
∵DH⊥OD,
∴设直线DH的解析式为![]() ,
,
将点D(2,1)的坐标代入得![]() ,
,
解得:![]() ,
,
∴直线DH的解析式为![]() ,
,
∴“隔离直线”的表达式为![]() ;
;
(3)如图:
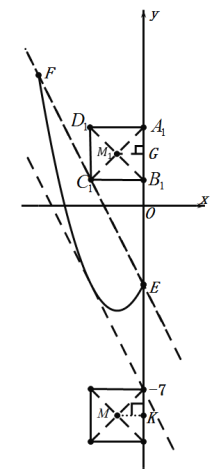
由题意点F的坐标为(![]() ),
),
当直线![]() 经过点F时,
经过点F时,![]() ,
,
∴![]() ,
,
∴直线![]() ,即图中直线EF,
,即图中直线EF,
∵正方形A1B1C1D1的中心M(1,t),
过点![]() 作
作![]() ⊥y轴于点G,
⊥y轴于点G,
∵点![]() 是正方形的中心,且
是正方形的中心,且![]() ,
,
∴B1C1![]() ,
,![]() ,
,
∴正方形A1B1C1D1的边长为2,
当![]() 时,
时,![]() ,
,
∴点C1的坐标是(![]() ),此时直线EF是函数
),此时直线EF是函数![]() )的图象与正方形A1B1C1D1的“隔离直线”,
)的图象与正方形A1B1C1D1的“隔离直线”,
∴点![]() 的坐标是(-1,2),
的坐标是(-1,2),
此时![]() ;
;
当直线![]() 与
与![]() 只有一个交点时,
只有一个交点时,
![]() ,消去y得到
,消去y得到![]() ,
,
由![]() ,可得
,可得![]() ,
,
解得:![]() ,
,
同理,此时点M的坐标为:(![]() ),
),
∴![]() ,
,
根据图象可知:
当![]() 或
或![]() 时,直线
时,直线![]() 是函数
是函数![]() )的图象与正方形A1B1C1D1的“隔离直线”.
)的图象与正方形A1B1C1D1的“隔离直线”.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】![]() 内接于
内接于![]() 边于点
边于点![]() ,连接
,连接![]() .
.
![]() 如图1,求证:
如图1,求证:![]() ;
;
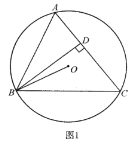
![]() 如图2,延长
如图2,延长![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上,射线
上,射线![]() 交
交![]() 边于点
边于点![]() ,连接
,连接![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
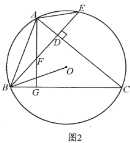
![]() 如图3,在
如图3,在![]() 的条件下,连接
的条件下,连接![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上运动,且
轴的正半轴上运动,且![]() ,下列结论:
,下列结论:
①![]()
②当![]() 时四边形
时四边形![]() 是正方形
是正方形
③四边形![]() 的面积和周长都是定值
的面积和周长都是定值
④连接![]() ,
,![]() ,则
,则![]() ,其中正确的有( )
,其中正确的有( )
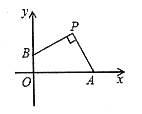
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
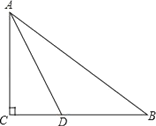
(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD=2![]() ,∠CAD=30°时,求劣弧AD的长.
,∠CAD=30°时,求劣弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=-![]() x+3交于C、D两点.连接BD、AD.
x+3交于C、D两点.连接BD、AD.

(1)求m的值.
(2)抛物线上有一点P,满足S△ABP=4S△ABD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 内接于⊙
内接于⊙![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() ,满足
,满足![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() ,
,![]() =
=![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 为
为![]() 上一点,分别连接
上一点,分别连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交⊙
,交⊙![]() 于点
于点![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长.
的长.
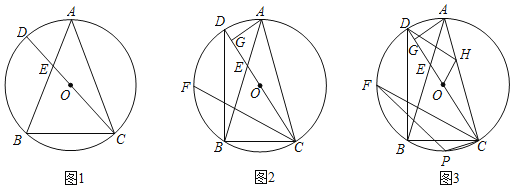
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷,在一次购物中,张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.
(1)张华用“微信”支付的概率是______.
(2)请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com