
【题目】已知二次函数![]() 的图象和
的图象和![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是直线
是直线![]() 上方的抛物线上的动点.
上方的抛物线上的动点.
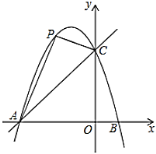
(1)求直线![]() 的解析式.
的解析式.
(2)当![]() 是抛物线顶点时,求
是抛物线顶点时,求![]() 面积.
面积.
(3)在![]() 点运动过程中,求
点运动过程中,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3)![]() 面积的最大值为
面积的最大值为![]() .
.
【解析】
(1)由题意分别将x=0、y=0代入二次函数解析式中求出点C、A的坐标,再根据点A、C的坐标利用待定系数法即可求出直线AC的解析式;
(2)由题意先根据二次函数解析式求出顶点![]() ,进而利用割补法求
,进而利用割补法求![]() 面积;
面积;
(3)根据题意过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() 并设点
并设点![]() 的坐标为
的坐标为![]() (
(![]() ),则点
),则点![]() 的坐标为
的坐标为![]() 进而进行分析.
进而进行分析.
解:(1) 分别将x=0、y=0代入二次函数解析式中求出点C、A的坐标为![]() ;
;![]() ;
;
将![]() ;
;![]() 代入
代入![]() ,得到直线
,得到直线![]() 的解析式为
的解析式为![]() .
.
(2)由![]() ,将其化为顶点式为
,将其化为顶点式为![]() ,可知顶点P为
,可知顶点P为![]() ,
,
如图P为顶点时连接PC并延长交x轴于点G,
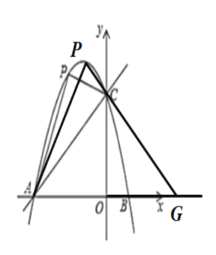
则有![]() ,
,
将P点和C点代入求出PC的解析式为![]() ,解得G为
,解得G为![]() ,
,
所有![]()
![]() =3;
=3;
(3)过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() .
.
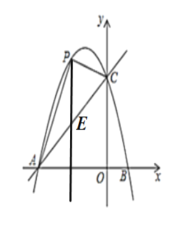
设点![]() 的坐标为
的坐标为![]() (
(![]() ),则点
),则点![]() 的坐标为
的坐标为![]()
∴![]()
![]() ,
,
当![]() 时,
时,![]() 取最大值,最大值为
取最大值,最大值为![]() .
.
∵![]() ,
,
∴![]() 面积的最大值为
面积的最大值为![]() .
.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为P,且与y轴交于点A,与直线
的顶点为P,且与y轴交于点A,与直线![]() 交于点B,C(点B在点C的左侧).
交于点B,C(点B在点C的左侧).
(1)求抛物线![]() 的顶点P的坐标(用含a的代数式表示);
的顶点P的坐标(用含a的代数式表示);
(2)横、纵坐标都是整数的点叫做整点,记抛物线与线段AC围成的封闭区域(不含边界)为“W区域”.
①当![]() 时,请直接写出“W区域”内的整点个数;
时,请直接写出“W区域”内的整点个数;
②当“W区域”内恰有2个整点时,结合函数图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
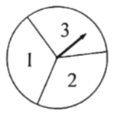
【题目】如图,有一个三等分数字转盘,小红先转动转盘,指针指向的数字记下为![]() ,小芳后转动转盘,指针指向的数字记下为
,小芳后转动转盘,指针指向的数字记下为![]() ,从而确定了点
,从而确定了点![]() 的坐标
的坐标![]() ,(若指针指向分界线,则重新转动转盘,直到指针指向数字为止)
,(若指针指向分界线,则重新转动转盘,直到指针指向数字为止)
(1)小红转动转盘,求指针指向的数字2的概率;
(2)请用列举法表示出由![]() ,
,![]() 确定的点
确定的点![]() 所有可能的结果.
所有可能的结果.
(3)求点![]() 在函数
在函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀的传统文化,市教育局决定开展“经典诵读进校园”活动,某校园团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表:
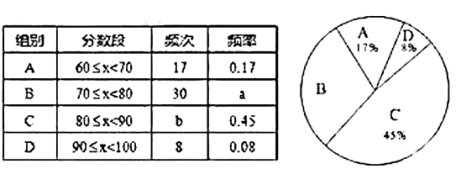
请根据所给信息,解答以下问题:
(1)表中![]() ;
;![]() ;
;
(2)请计算扇形统计图中![]() 组对应的圆心角的度数;
组对应的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列举法或树状图法求甲、乙两名同学都被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() , 记
, 记![]() ,点
,点![]() 为射线
为射线![]() 上的动点,连接
上的动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角后得到射线
角后得到射线![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 交于点
交于点![]() ,点
,点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
(1)当![]() 为等边三角形时,
为等边三角形时,
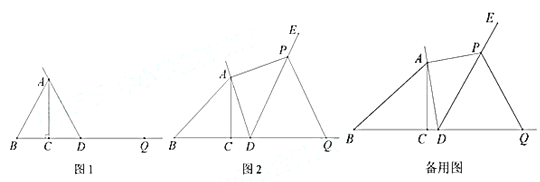
① 依题意补全图1;
②![]() 的长为________;
的长为________;
(2)如图2,当![]() ,且
,且![]() 时, 求证:
时, 求证:![]() ;
;
(3)设![]() , 当
, 当![]() 时,直接写出
时,直接写出![]() 的长. (用含
的长. (用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
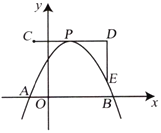
【题目】如图,一抛物线与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,其顶点
两点,其顶点![]() 在折线段
在折线段![]() 上移动,已知点
上移动,已知点![]() ,
,![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,若点
,若点![]() 横坐标的最小值为0,则点
横坐标的最小值为0,则点![]() 横坐标的最大值为______.
横坐标的最大值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
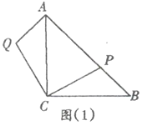
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
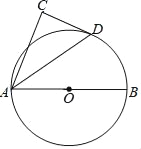
【题目】如图,AB为⊙O的直径,D为⊙O上一点,以AD为斜边作△ADC,使∠C=90°,∠CAD=∠DAB
(1)求证:DC是⊙O的切线;
(2)若AB=9,AD=6,求DC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com