
【题目】在![]() 中,
中,![]() , 记
, 记![]() ,点
,点![]() 为射线
为射线![]() 上的动点,连接
上的动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角后得到射线
角后得到射线![]() ,过点
,过点![]() 作
作![]() 的垂线,与射线
的垂线,与射线![]() 交于点
交于点![]() ,点
,点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
(1)当![]() 为等边三角形时,
为等边三角形时,
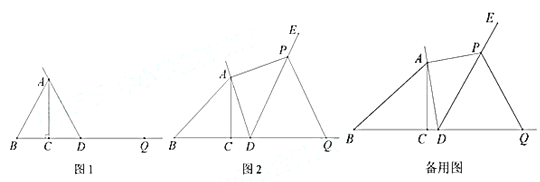
① 依题意补全图1;
②![]() 的长为________;
的长为________;
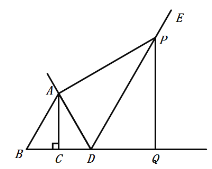
(2)如图2,当![]() ,且
,且![]() 时, 求证:
时, 求证:![]() ;
;
(3)设![]() , 当
, 当![]() 时,直接写出
时,直接写出![]() 的长. (用含
的长. (用含![]() 的代数式表示)
的代数式表示)
【答案】(1)①见解析,②![]() . (2)见解析;(3)
. (2)见解析;(3)![]() .
.
【解析】
(1)①根据题意补全图形即可;
②根据旋转的性质和对称的性质易证得![]() ,利用特殊角的三角函数值即可求得答案;
,利用特殊角的三角函数值即可求得答案;
(2)作![]() 于
于![]() ,
,![]() 于
于![]() ,证得四边形
,证得四边形![]() 是矩形,求得
是矩形,求得![]() ,再证得
,再证得![]() ,求得
,求得![]() ,再求得
,再求得![]() ,即可证得结论.
,即可证得结论.
(3)设![]() 则
则![]() ,证得
,证得![]() ,求得
,求得![]() ,再作DM⊥AB,PN⊥DQ,利用面积法求得
,再作DM⊥AB,PN⊥DQ,利用面积法求得![]() ,继而求得
,继而求得![]() ,再证得
,再证得![]() ,求得
,求得![]() ,根据
,根据![]() 得
得![]() ,即可求得答案.
,即可求得答案.
(1)解:①补全图形如图所示:
②∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
根据旋转的性质和对称的性质知:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,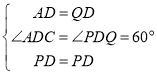 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为等边三角形,
为等边三角形,![]() ,
,
∴ ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
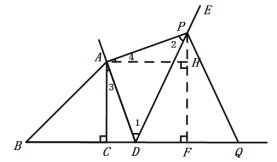
∵![]() ,
,
∴![]() ,
,
由题意可知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 关于点
关于点![]() 对称,
对称,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为
为![]() 中点,
中点,
∴![]() 垂直平分
垂直平分![]() ,
,
∴![]() ;
;
(3)∵![]() ,AC⊥BD,
,AC⊥BD,
∴![]() ,
,
设![]() 则
则![]() ,
,
∵AC⊥BD,AP⊥AD,
∴∠ACB=∠PAD![]() ,
,
又∵∠ABC=∠PDA![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴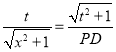 ,
,
∴![]() ,
,
作DM⊥AB,PN⊥DQ,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴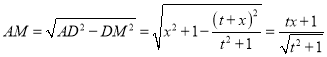 ,
,
∵![]() ,
,
又∵∠AB![]() =∠PDA
=∠PDA![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴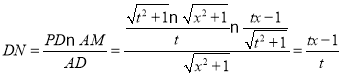 ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,半径OC⊥AB于O,AD平分∠CAB交![]() 于点D,连接CD,OD,BD.下列结论中正确的是( )
于点D,连接CD,OD,BD.下列结论中正确的是( )

A.AC∥ODB.![]()
C.△ODE∽△ADOD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长60 cm、宽40 cm的长方形风景画的四周镶一条金色纸边,制成一幅长方形挂图,如图.如果要使整个挂图的面积是2816 cm2,设金色纸边的宽为x cm,那么x满足的方程是( )

A. (60+2x)(40+2x)=2816
B. (60+x)(40+x)=2816
C. (60+2x)(40+x)=2816
D. (60+x)(40+2x)=2816
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象和
的图象和![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是直线
是直线![]() 上方的抛物线上的动点.
上方的抛物线上的动点.
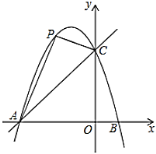
(1)求直线![]() 的解析式.
的解析式.
(2)当![]() 是抛物线顶点时,求
是抛物线顶点时,求![]() 面积.
面积.
(3)在![]() 点运动过程中,求
点运动过程中,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“红灯停,绿灯行”是我们过路口遇见交通信号灯时必须遵守的规则.小明每天从家骑自行车上学要经过三个路口,假如每个路口交通信号灯中红灯和绿灯亮的时间相同,且每个路口的交通信号灯只安装了红灯和绿灯.那么某天小明从家骑车去学校上学,经过三个路口抬头看到交通信号灯.
(1)请画树状图,列举小明看到交通信号灯可能出现的所有情况;
(2)求小明途经三个路口都遇到红灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
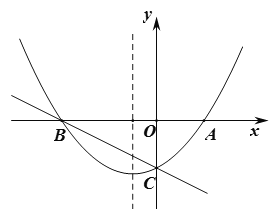
【题目】如图,对称轴是![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 若点
若点![]() 是直线
是直线![]() 下方的抛物线上的动点,求
下方的抛物线上的动点,求![]() 的面积的最大值;
的面积的最大值;
![]() 若点
若点![]() 在抛物线对称轴左侧的抛物线上运动,过点
在抛物线对称轴左侧的抛物线上运动,过点![]() 作
作![]() 铀于点
铀于点![]() ,交直线
,交直线![]() 于点
于点![]() ,且
,且![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在对称轴上是否存在一点
在对称轴上是否存在一点![]() ,使
,使![]() 的周长最小,若存在,请求出
的周长最小,若存在,请求出![]() 点的坐标和
点的坐标和![]() 周长的最小值;若不存在,请说明理由.
周长的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com