练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
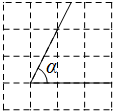
    6．如图，在4×4的正方形网格中，tanα的值等于（　　）
    A．2B．$\frac{1}{2}$C．$\frac{{\sqrt{5}}}{5}$D．$\frac{{2\sqrt{5}}}{5}$

    分析 求一个角的正切值，可将其转化到直角三角形中，利用直角三角函数关系解答．

    解答 解：如图，tanα=$\frac{AC}{BC}$=2，
    故选：A．

    点评 本题考查的是锐角三角函数的定义，掌握在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．多项式-2ab+4a3b-a2b3+1的次数是5，二次项系数是-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．若x表示一个两位数，把数字3放在x的右边，组成一个三位数是（　　）
    A．3xB．10x+3C．100x+3D．3×100+x

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．先化简，再求值：$\frac{a^3}{{{a^2}-2a+1}}÷（{1-\frac{1}{1-a}}）$，其中a2+a-1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九2x=-6章算术》中记载：“今有人共买鸡，人出九，盈十一；人出六，不足十六．问人数、鸡价各几何？”
    译文：“假设有几个人共同出钱买鸡，如果每人出九钱，那么多了十一钱；
    如果每人出六钱，那么少了十六钱．问：有几个人共同出钱买鸡？鸡的价
    钱是多少？”
    设有x个人共同买鸡，根据题意列一元一次方程，正确的是（　　）
    A．9x+11=6x-16B．9x-11=6x+16C．$\frac{x-11}{9}=\frac{x+16}{6}$D．$\frac{x+11}{9}=\frac{x-16}{6}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

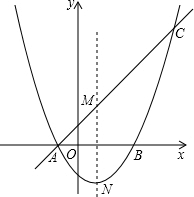    2．如图，抛物线y=$\frac{1}{2}$x2+mx+n交x轴于A、B两点，直线y=kx+b经过点A，与这条抛物线的对称轴交于点M（1，2），且点M与抛物线的顶点N关于x轴对称．
    （1）求这条抛物线的函数关系式；
    （2）设抛物线与直线的另一交点为C，已知P为线段AC上一点（不含端点），过点P作PQ⊥x轴，交抛物线于点Q，设点P的横坐标为x，用含x的代数式表示线段PQ的长，并求出PQ的最大值；
    （3）若点D在抛物线的对称轴上，点E在抛物线上，是否存在以A、B、D、E为顶点的四边形为平行四边形？若存在，求出点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

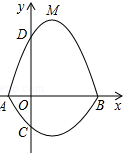    9．如图，在平面直角坐标系xOy中，A、B为x轴上两点，C、D为y轴上的两点，经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封闭曲线成为“蛋线”．已知点C的坐标为（0，-$\frac{3}{2}$），点M是抛物线C2：y=mx2-2mx-3m（m＜0）的顶点．
    （1）求A、B两点的坐标；
    （2）当△BDM为以∠M为直角的直角三角形时，求m的值．
    （3）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，将等腰Rt△ABC放置在平面直角坐标系中，∠CAB=90°，AC=AB．
    （1）如图1，点B，C分别在x，y轴上，求证：点A在∠BOC的角平分线上；
    （2）如图2，已知A（3，0），C（0，4），求点B的坐标；
    （3）如图3，点A，C分别在x，y轴上，点E为BC上一点，以AE为边作等腰Rt△AED，∠AED=90°，连接CD，求∠ACD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．抛物线y=-2（x+1）2-2的顶点坐标是（-1，-2）．

    查看答案和解析>>

    同步练习册答案