
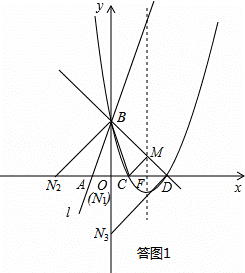
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
 (3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
解:(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(﹣1,0),B(0,3);
 ∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0).
∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴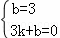 ,
,
解得k=﹣1,b=3,
∴直线BD的解析式为:y=﹣x+3.
设抛物线的解析式为:y=a(x﹣1)(x﹣3),
∵点B(0,3)在抛物线上,
∴3=a×(﹣1)×(﹣3),
解得:a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3.……4分
(2)抛物线的解析式为:y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,﹣1).
直线BD:y=﹣x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MN=1,
∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
如答图1所示:
(I)若BD为斜边,则易知此时直角顶点为原点O,
 ∴N1(0,0);
∴N1(0,0);
(II)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(﹣3,0);
(III)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,﹣3).
∴满足条件的点N坐标为:(0,0),(﹣3,0)或(0,﹣3).
…………………………6分
(3)假设存在点P,使S△PBD=6,设点P坐标为(m,n).
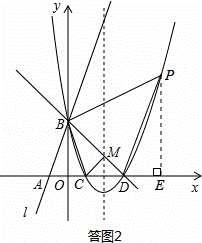
(I)当点P位于直线BD上方时,如答图2所示:
过点P作PE⊥x轴于点E,则PE=n,DE=m﹣3.
S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=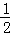 (3+n)•m﹣
(3+n)•m﹣ ×3×3﹣
×3×3﹣ (m﹣3)•n=6,
(m﹣3)•n=6,
化简得:m+n=7 ①,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入①式整理得:m2﹣3m﹣4=0,
 解得:m1=4,m2=﹣1,
解得:m1=4,m2=﹣1,
∴n1=3,n2=8,
∴P1(4,3),P2(﹣1,8);
(II)当点P位于直线BD下方时,如答图3所示:
过点P作PE⊥y轴于点E,则PE=m,OE=﹣n,BE=3﹣n.
S△PBD=S梯形PEOD+S△BOD﹣S△PBE
=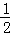 (3+m)•(﹣n)+
(3+m)•(﹣n)+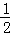 ×3×3﹣
×3×3﹣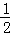 (3﹣n)•m=6,
(3﹣n)•m=6,
化简得:m+n=﹣1 ②,
∵P(m,n)在抛物线上,
∴n=m2﹣4m+3,
代入②式整理得:m2﹣3m+4=0,△=﹣7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(﹣1,8).


科目:初中数学 来源: 题型:
如图,已知斜坡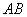 长60米,坡角(即
长60米,坡角(即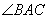 )为30°,
)为30°,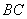 ⊥
⊥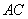 ,现计划在斜坡中点
,现计划在斜坡中点 处挖去部分坡体(用阴影表示)修建一个平行于水平线
处挖去部分坡体(用阴影表示)修建一个平行于水平线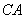 的平台
的平台 和一条新的斜坡
和一条新的斜坡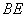 .
.
(1)若修建的斜坡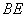 的坡角(即
的坡角(即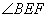 )不大于45°,则平台
)不大于45°,则平台 的长最多为多少米?
的长最多为多少米?
(2)一座建筑物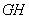 距离坡角
距离坡角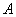 点27米远(即
点27米远(即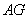 =27米),小明在
=27米),小明在 点测得建筑物顶部
点测得建筑物顶部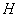 的仰角(即
的仰角(即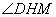 )为30°,点
)为30°,点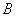 、
、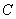 、
、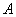 、
、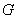 、
、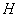 在同一个平面内,点
在同一个平面内,点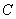 、
、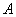 、
、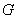 在同一条直线上,且
在同一条直线上,且

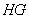 ⊥
⊥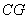 ,问建筑物
,问建筑物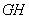 高为多少米?
高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com