
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
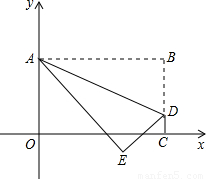
(1)当m=3时,点B的坐标为 ,点E的坐标为 ;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
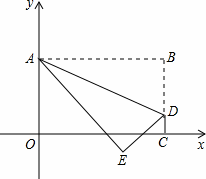
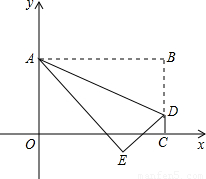
(3)如图,若点E的纵坐标为-1,抛物线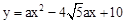 (a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
(a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
解:(1)点B的坐标为(3,4),点E的坐标为(0,1)。
(2)点E能恰好落在x轴上。理由如下:
∵四边形OABC为矩形,∴BC=OA=4,∠AOC=∠DCE=90°。
由折叠的性质可得:DE=BD=OA-CD=4-1=3,AE=AB=OC=m。
如图1,假设点E恰好落在x轴上,
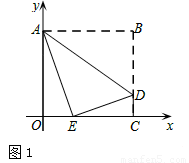
在Rt△CDE中,由勾股定理可得
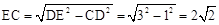 ,
,
则有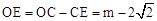 。
。
在Rt△AOE中,OA2+OE2=AE2,
即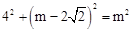 ,解得
,解得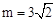 。
。
(3)如图2,过点E作EF⊥AB于F,EF分别与AD、OC交于点G、H,过点D作DP⊥EF于点P,则EP=PH+EH=DC+EH=2,
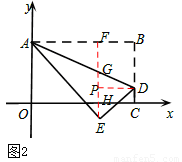
在Rt△PDE中,由勾股定理可得
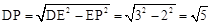 ,
,
∴BF=DP=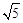 。
。
在Rt△AEF中,AF=AB−BF=m−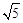 ,EF=5,AE=m,
,EF=5,AE=m,
∵AF2+EF2=AE2,即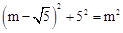 ,解得m=3
,解得m=3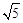 。
。
∴AB=3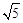 ,AF=2
,AF=2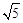 ,E(2
,E(2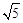 ,-1)。
,-1)。
∵∠AFG=∠ABD=90°,∠FAG=∠BAD,∴△AFG∽△ABD。
∴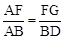 ,即
,即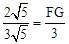 ,解得FG=2。∴EG=EF-FG=3。∴点G的纵坐标为2。
,解得FG=2。∴EG=EF-FG=3。∴点G的纵坐标为2。
∵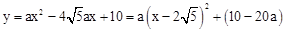 ,
,
∴此抛物线的顶点必在直线x=2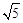 上。
上。
又∵抛物线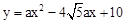 的顶点落在△ADE的内部,
的顶点落在△ADE的内部,
∴此抛物线的顶点必在EG上。
∴-1<10-20a<2,解得 。
。
∴a的取值范围为 。
。
【解析】
试题分析:(1)根据点A、点D、点C的坐标和矩形的性质可以得到点B和点E的坐标。
(2)由折叠的性质求得线段DE和AE的长,然后利用勾股定理得到有关m的方程,求得m的值即可。
(3)过点E作EF⊥AB于F,EF分别与 AD、OC交于点G、H,过点D作DP⊥EF于点P,首先利用勾股定理求得线段DP的长,从而求得线段BF的长,再利用△AFG∽△ABD得到比例线段求得线段FG的长,最后求得a的取值范围。


科目:初中数学 来源: 题型:
 (2013•晋江市)将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(2013•晋江市)将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为 ,点E的坐标为 ;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
(3)如图,若点E的纵坐标为-1,抛物线![]() (a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
(a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013年福建省泉州市晋江市初中学业质量检查数学试卷(二)(解析版) 题型:解答题
 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.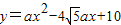 (a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
(a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.查看答案和解析>>
科目:初中数学 来源:2013年福建省泉州市晋江市中考数学试卷(解析版) 题型:解答题
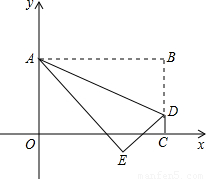 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.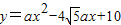 (a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.
(a≠0且a为常数)的顶点落在△ADE的内部,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com