

| x | … | -7 | -6 | -4 | -3 | -2 | -1 | 0 | 1 | 3 | 4 | … |
| y | … | 5.477… | 4.472… | 2.449… | 1.414… | 0 | 0 | 1.414… | 2.449… | 4.472… | 5.477… | … |
分析 (1)当抛物线在x轴上方部分进满足条件,可确定出对应的x的取值范围;
(2)①由二次根式的意义可得到(x+1)(x+2)≥0,可转化为(1);②利用描点法可画出函数图象;③结合图象可得出答案.
解答 解:
(1)x2+3x+2>0的解集即抛物线在x轴上方部分对应的自变量的取值范围,
∴x<-2或x>-1,
故答案为:<-2或x>-1;
(2)①由题意可得(x+1)(x+2)≥0,
由(1)可得x≤-2或x≥-1,
故答案为:x≤-2或x≥-1;
②如图: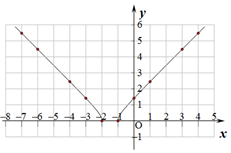
③由图象可知关于直线x=-1.5对称,
故答案为:关于直线x=-1.5对称.
点评 本题主要考查二次函数的性质及函数与方程不等式的关系,利用数形结合是解题的关键.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3<h<5 | B. | 5<h<10 | C. | 10<h<15 | D. | 15<h<20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 无数条 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a2-(2a-b+5c)=3a2-2a+b-5c | B. | 5x2+(-2x+y)-(3z-a)=5x2-2x+y-3z+a | ||
| C. | 2m2-3(m-1)=2m2-3m-1 | D. | -(2x-y)-(-x2+y2)=-2x+y+x2-y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com