【题目】互联网给生活带来极大的方便据报道，2016底全球支付宝用户数为4.5亿，2018年底达到9亿．
（1）求平均每年增长率；
（2）据此速度，2020底全球支付宝用户数是否会超过17亿？请说明理由．（参考数据：
≈1.414）
【答案】(1) 41.4%;(2)见解析.
【解析】
（1）设平均每年增长率为x，根据2016年底及2018年底全球支付宝用户数，即可得出关于x的一元二次方程，解之取其正值即可得出结论；
（2）根据2020年底全球支付宝用户数=2018年底全球支付宝用户数×（1+增长率）2，即可求出2020年底全球支付宝用户数，将其与17亿比较后即可得出结论．
（1）设平均每年增长率为x，
依题意，得：4.5（1+x）2＝9，
解得：x1＝0.414＝41.4%，x2＝﹣2.414（舍去）．
答：平均每年增长率为41.4%．
（2）9×（1+41.4%）2≈17.995（亿）．
∵17.995＞17，
∴2020底全球支付宝用户数会超过17亿．
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】为了丰富校园文化生活，某校计划在午间校园广播台播放“百家讲坛”的部分内容为了了解学生的喜好，抽取若干名学生进行问卷调查（每人只选一项内容），整理调查结果，绘制统计图如下：
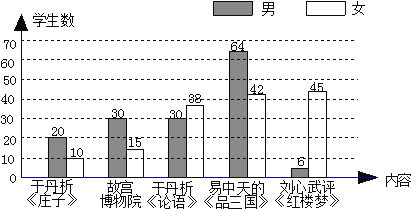
请根据统计图提供的信息回答以下问题：
（1）这一调查属于_______（选填“抽样调查”或“普查”），抽取的学生数为_____名；
（2）估计喜欢收听易中天《品三国》的学生约占全校学生的____%（精确到小数点后一位）；
（3）已知该校女学生共有1800名，则该校喜欢收听刘心武评《红楼梦》的女学生大约有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，
是矩形
内部的一定点，
是
边上一动点，连接
并延长与矩形的一边交于点
，连接
．已知
，设
，两点间的距离为
，，两点间的距离为
，，两点间的距离为
．小欣根据学习函数的经验，分别对函数
，
随自变量
的变化而变化的规律进行了探究．下面是小欣的探究过程，请补充完整；
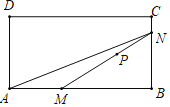
(1)按照如表中自变量的值进行取点、画图、测量，分别得到了，与的几组对应值；
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 6.30 | 5.40 | ______ | 4.22 | 3.13 | 3.25 | 4.52 |
| 6.30 | 6.34 | 6.43 | 6.69 | 5.75 | 4.81 | 3.98 |
(2)在同一平面直角坐标系
中，描出以补全后的表中各组对应值所对应的点
，并画出函数的图象；
(3)结合函数图象，解决问题：当
为等腰三角形时，
的长度约为______
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知如图，在△ABC中，∠B＝45°，点D是BC边的中点，DE⊥BC于点D，交AB于点E，连接CE．
（1）求∠AEC的度数；
（2）请你判断AE、BE、AC三条线段之间的等量关系，并证明你的结论．
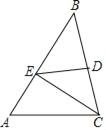
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是（ ）
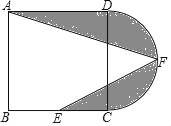
A. 18+36π B. 24+18π C. 18+18π D. 12+18π
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行．某自行车店在销售某型号自行车时，以高出进价的50%标价．已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同．
（1）求该型号自行车的进价和标价分别是多少元？
（2）若该型号自行车的进价不变，按（1）中的标价出售，该店平均每月可售出51辆；若每辆自行车每降价20元，每月可多售出3辆，求该型号自行车降价多少元时，每月获利最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
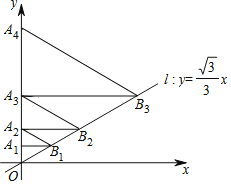
【题目】如图，直线L：y＝
x，点A坐标为（0，1），过点A作y轴的垂线交直线L于点B1以OB1为边作等边三角形OA1B1，再过点A1作y轴的垂线交直线L于点B2，以OB2为边作等边三角形OA2B2，……，按此做法进行下去，点A2019的坐标为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
