
 如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,使顶点B的对应点B′落在直角边AC的中点上,求CE的长.
如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,使顶点B的对应点B′落在直角边AC的中点上,求CE的长.  中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:解答题
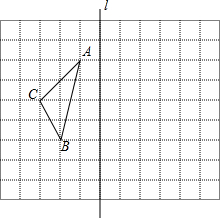 如图所示的方格纸中,每一个小正方形的边长都是1,网格中有一个格点三角形ABC.
如图所示的方格纸中,每一个小正方形的边长都是1,网格中有一个格点三角形ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一副三角板的两个直角顶点重合在一起.
如图,一副三角板的两个直角顶点重合在一起.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 若平面直角坐标系中的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.规定“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
若平面直角坐标系中的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.规定“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com