
如图,抛物线 与x轴交于A(
与x轴交于A(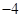 ,0)、B(3,0)两点,与y轴交于点C.
,0)、B(3,0)两点,与y轴交于点C.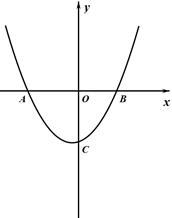
(1)求抛物线的函数关系式;
(2)点P是抛物线上第三象限内的一动点,当点P运动到什么位置时,四边形ABCP的面积最大?求出此时点P的坐标和四边形ABCP的面积;
(3)点M在抛物线对称轴上,点N是平面内一点,是否存在这样的点M、N,使得以点M、N、B、C为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
(1)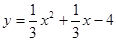 (2)四边形ABCP的面积的最大值为
(2)四边形ABCP的面积的最大值为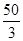 ,点P坐标为
,点P坐标为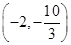 (3)存在;
(3)存在; M1(
M1(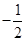 ,
,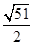 ) M2(
) M2(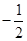 ,
,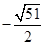 ) M3(
) M3(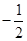 ,
,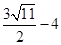 ) M4 (
) M4 (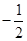 ,
,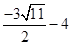 ) M5(
) M5(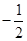 ,
,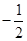 )
)
解析试题分析:⑴抛物线 与x轴交于A(
与x轴交于A(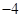 ,0)、B(3,0)两点,则
,0)、B(3,0)两点,则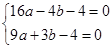 ;解得
;解得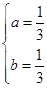 ,所以抛物线的解析式是
,所以抛物线的解析式是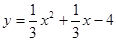
⑵过P点做PD垂直于X轴;四边形ABCP的面积=三角形OBC的面积+三角形APD的面积+梯形OCPD的面积;抛物线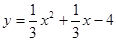 与y轴的交点是C,C的坐标(0,y)解得y=-4,则OC=4,而OC是三角形ABC的高;抛物线
与y轴的交点是C,C的坐标(0,y)解得y=-4,则OC=4,而OC是三角形ABC的高;抛物线 与x轴交于A(
与x轴交于A(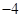 ,0)、B(3,0)两点,OC=3,则
,0)、B(3,0)两点,OC=3,则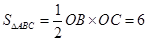 ;设P点的坐标为(x,y); 点P是抛物线上第三象限内的一动点,PD="-y,OD=-x;" 则
;设P点的坐标为(x,y); 点P是抛物线上第三象限内的一动点,PD="-y,OD=-x;" 则
 =
=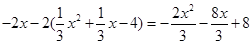 =
=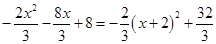
当x+2=0即x=-2时四边形ABCP的面积的最大值为=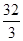 +6=
+6=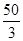
点P坐标为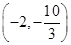
⑶点M在抛物线对称轴上,抛物线的函数关系式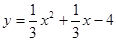 ,其对称轴X=
,其对称轴X=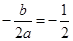 ;在直角三角形OBC中BC=5;点N是平面内一点,使得以点M、N、B、C为顶点的四边形是菱形,根据菱形的性质四边相等解得
;在直角三角形OBC中BC=5;点N是平面内一点,使得以点M、N、B、C为顶点的四边形是菱形,根据菱形的性质四边相等解得
M1(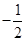 ,
,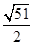 ) M2(
) M2(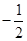 ,
,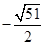 ) M3(
) M3(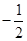 ,
,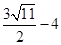 ) M4 (
) M4 (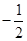 ,
,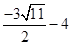 )
)
M5(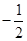 ,
,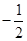 )
)
考点:二次函数
点评:考查二次函数的知识,本题要求学生掌握用待定系数法求二次函数的解析式,本题难度较大,但(1)小问比较简单,要求学生会做,后面两小问,难度较大,要求中等成绩以上的学生要会做


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是| 10 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com