
 ;
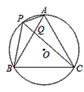
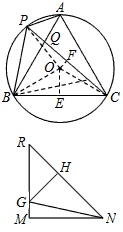
;| 解:(1)∵∠ABC=∠APC=60°,∠BAC=∠BPC=60°, ∴∠ACB=180°-∠ABC-∠BAC=60°, ∴△ABC是等边三角形; (2)如图,过B作BD∥PA交PC于D,则∠BDP=∠APC=60°, 又∵∠AQP=∠BQD, ∴△AQP∽△BQD, 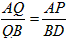 , ,∵∠BPD=∠BDP=60°, ∴PB=BD, ∴ 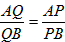 ; ;(3)设正△ABC的高为h,则h=BC·sin60°, ∵ 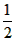 BC·h=4 BC·h=4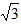 ,即 ,即 BC·BC·sin60°=4 BC·BC·sin60°=4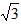 ,解得BC=4, ,解得BC=4,连接OB,OC,OP,作OE⊥BC于E, 由△ABC是正三角形知∠BOC=120°,从而得∠OCE=30°, ∴ 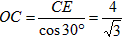 , ,由∠ABP=15°得∠PBC=∠ABC+∠ABP=75°,于是∠POC=2∠PBC=150°, ∴∠PCO=(180°-150°)÷2=15°, 如图,作等腰直角△RMN,在直角边RM上取点G, 使∠GNM=15°,则∠RNG=30°,作GH⊥RN,垂足为H, 设GH=1,则cos∠GNM=cos15°=MN, ∵在Rt△GHN中,NH=GN·cos30°,GH=GN·sin30°, 于是RH=GH,MN=RN·sin45°, ∴cos15°= 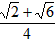 , ,在图中,作OF⊥PC于E, ∴PC=2FD=2OC·cos15°= 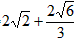 。 。 |
 |


科目:初中数学 来源: 题型:
 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=| 4 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com