
����Ŀ��ij��ѧ��ί��֯���Ļ�����������ɽ��ѧУ�ƻ����˸����轱���ȥ����![]() ���ֽ�Ʒ��
���ֽ�Ʒ��![]() ��������
��������![]() �ͽ�Ʒ������
�ͽ�Ʒ������![]() �ͽ�Ʒ������
�ͽ�Ʒ������![]() ����
����![]() ����
����![]() �ͽ�Ʒ�������ò�����
�ͽ�Ʒ�������ò�����![]() �ͽ�Ʒ�������õ�
�ͽ�Ʒ�������õ�![]() �������ֽ�Ʒ�ĵ������ұ���ʾ������ƻ�
�������ֽ�Ʒ�ĵ������ұ���ʾ������ƻ�![]() �ͽ�Ʒ��
�ͽ�Ʒ��![]() ������
������![]() ����Ʒ���ܷ�����
����Ʒ���ܷ�����![]() Ԫ��
Ԫ��
|
|
| |
����(Ԫ) |
|
|
|
��1������![]() ��
��![]() ֮��ĺ�����ϵʽ��������Ա���
֮��ĺ�����ϵʽ��������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���������һ�ַ�����ʹ�ù��������ֽ�Ʒ�������ܷ������٣���������ٷ��ã�
���𰸡���1��![]() ��
��![]() ������2������
������2������![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() �������ٷ���Ϊ
�������ٷ���Ϊ![]() Ԫ
Ԫ
��������
(1)�����������B�ͽ�Ʒ��2x-10������C�ͽ�Ʒ��60-3x�������г���ʽw=12x+10��2x-10��+5��60-3x�����ɣ��������ʽ��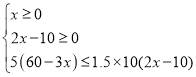 �Ľ⼯���ٸ���A�ͽ�Ʒ��B�ͽ�Ʒ�ĺ�ҪС������50����������𰸣�
�Ľ⼯���ٸ���A�ͽ�Ʒ��B�ͽ�Ʒ�ĺ�ҪС������50����������𰸣�
(2) ����һ�κ������������xȡ��Сʱw��ֵ���ɣ�
![]() �������
�������![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����
![]() ��
��
��������õ�����ʽ�飺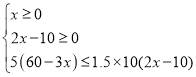
���x��10��
��A�ͽ�Ʒ��B�ͽ�Ʒ�ĺ�ҪС��50����
��x+2x-10��50��
��x��20��
���Ա���x��ȡֵ��Χ��10��x��20��
��w��x֮��ĺ�����ϵʽ��w=17x+200���Ա���x��ȡֵ��Χ��10��x��20��
![]() ��
��![]() ��
�У�
![]()
![]() ��
��![]() �ļ�С����С
�ļ�С����С
![]() ��
��![]() ʱ��
ʱ��![]() ȡ����Сֵ����СֵΪ
ȡ����Сֵ����СֵΪ![]()
��������![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����![]() �ͽ�Ʒ
�ͽ�Ʒ![]() ����
����
��ʹ���������ֽ�Ʒ�������ܷ������٣����ٷ���Ϊ![]() Ԫ��
Ԫ��
�𣺹���A�ͽ�Ʒ10����B�ͽ�Ʒ10����C�ͽ�Ʒ30������ʹ���������ֽ�Ʒ�������ܷ������٣����ٷ���Ϊ370Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
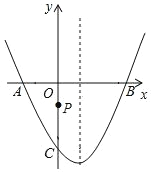
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ��� y��ax2+bx+c ��ͼ�� x ����A��B ���㣬�� y ���� C �㣬P Ϊ y ���ϵ�һ�����㣬��֪ A����2��0����C��0����2![]() �����������ߵĶԳ�����ֱ�� x��1��
�����������ߵĶԳ�����ֱ�� x��1��
(1)��˶��κ����Ľ���ʽ��
(2)���� PB���� ![]() PC+PB ����Сֵ�� ��
PC+PB ����Сֵ�� ��
(3)���� PA��PB��P ���˶����δ�ʱ��ʹ����APB��60��������� P �����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��Ͼɵ��ӻ���Ļ�ij�����Ϊ4�U3�����Ƕ�����Ӱͼ��ij�����Ϊ2.4�U1�����ڲ��ŵ�Ӱʱ���ӻ���Ļ���Ϸ����·����������ȿ��ĺ�ɫ���ӣ�
��1����ͼ���е��ӻ���ĻΪ20�磨����Ļ�Խ��߳��ȣ���
�ٸ���Ļ�ij��� �磬���� �磻
����֪����Ļ�˷ѱȣ���ɫ���ӵ�����������ӻ���Ļ�������������õ��ӻ���Ļ���˷ѱȣ�
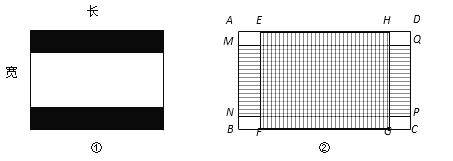
��2�� Ϊ�˼�˵�Ӱ����������һ���µ���Ļ�ij����ȵ����ˣ���ͼ�ڣ�������Ļ������ABCD��ǡ�ð����������ҳ����ȷֱ�Ϊ4�U3����Ļ������EFGH����2.4�U1����Ļ������MNPQ������������Ļ�ij����ȣ����ο����ݣ�![]() ��2.2�������ȷ��0.1��
��2.2�������ȷ��0.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
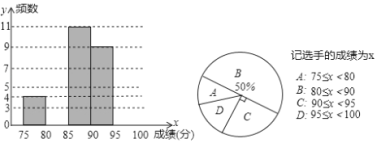
����Ŀ��ʤ����ѧΪ�ḻͬѧ�ǵ�У���������У����̨��������ѡ�������ֽ�36������ѡ�ֵijɼ�(��λ����)ͳ�Ʋ����Ƴ�Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ��������Ϣ���£�
�����ͳ��ͼ����Ϣ������������⣺
(1)��ȫƵ���ֲ�ֱ��ͼ��
(2)����ͳ��ͼ������A��Ӧ��Բ�ĽǶ���Ϊ��������
(3)�ɼ���D�����ѡ�֣�������Ů����һ�ˣ����������ȡ������ʱ���θ�У�����ڵ������ˣ���ǡ��ѡ��һ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
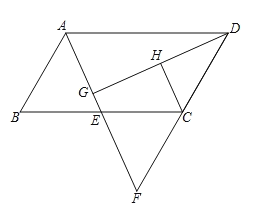
����Ŀ����ͼ���ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
��1����֤����![]() �ա�
�ա�![]() ��
��
��2������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() ���е㣮�ж�
���е㣮�ж�![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������ij��ʱ����Ʒÿ���ɱ�Ϊ![]() Ԫ�������г����з��֣�������Ʒ��δ��
Ԫ�������г����з��֣�������Ʒ��δ��![]() ���ڵ���������
���ڵ���������![]() (��)��ʱ��
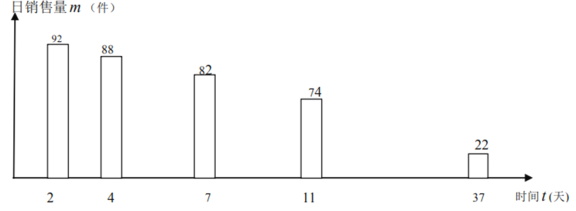
(��)��ʱ��![]() (��)�Ĺ�ϵ��ͼ��
(��)�Ĺ�ϵ��ͼ��
δ��![]() ���ڣ�ǰ
���ڣ�ǰ![]() ��ÿ��ļ۸�
��ÿ��ļ۸�![]() (Ԫ/��)��ʱ��
(Ԫ/��)��ʱ��![]() (��)�ĺ�����ϵʽΪ
(��)�ĺ�����ϵʽΪ![]() ����
����![]() ����)����
Ϊ����)����![]() ��ÿ��ļ۸�
��ÿ��ļ۸�![]() Ԫ/��(
Ԫ/��(![]() ����
����![]() Ϊ����)�������������о�����������Ʒ���й����⣺
Ϊ����)�������������о�����������Ʒ���й����⣺
��1���������ͼ�е����ݣ�����ѧ����һ�κ��������κ�����������������֪ʶȷ��һ��������Щ���ݵ�![]() (��)��
(��)��![]() (��)֮��Ĺ�ϵʽ��
(��)֮��Ĺ�ϵʽ��
��2����Ԥ��δ��![]() ������һ������������������������������Ƕ��٣�
������һ������������������������������Ƕ��٣�
��3����ʵ�����۵�ǰ![]() ���У��ù�˾����ÿ����һ����Ʒ�;���
���У��ù�˾����ÿ����һ����Ʒ�;���![]() Ԫ����
Ԫ����![]() ��ϣ�����̣���˾ͨ�����ۼ�¼���֣�ǰ
��ϣ�����̣���˾ͨ�����ۼ�¼���֣�ǰ![]() ��۳��������������������ʱ��
��۳��������������������ʱ��![]() (��)�������������
(��)�������������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
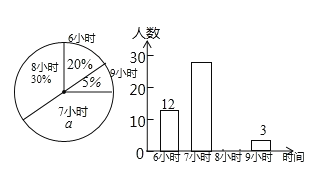
����Ŀ��Ϊ���˽�ijУ���и��꼶ѧ��ÿ���ƽ��˯��ʱ�䣨��λ��h����ȷ��1h�������������˲���ѧ�������õõ������ݻ���������������������ͳ��ͼ��
�������ͼ���ṩ����Ϣ���ش��������⣺
��1���������ͳ��ͼ�аٷ���a��ֵΪ�� ����������ѧ������Ϊ�� ����
��2�����ƽ��˯��ʱ��Ϊ8Сʱ������������ȫƵ��ֱ��ͼ��
��3������ⲿ��ѧ����ƽ��˯��ʱ���������ƽ������
��4�������У����ѧ��1200�����������˯�߲��㣨����8Сʱ����ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��x2+bx+c��ͼ����x���ཻ�ڵ�A��B����y���ཻ�ڵ�C��B�������Ϊ��6��0������MΪ�������ϵ�һ�����㣮
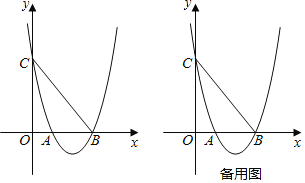
��1�����ö��κ���ͼ��ĶԳ���Ϊֱ��x��4ʱ��
������κ����ı���ʽ��
������Mλ��x���·�������ͼ����ʱ������M��x��Ĵ��ߣ���BC�ڵ�Q�����߶�MQ�����ֵ��
��2������M��BC��ƽ���ߣ����������ڵ�N�����M��N�ĺ�����Ϊm��n���ڵ�M�˶��Ĺ����У�����m+n��ֵ�Ƿ�ᷢ���ı䣿���ı䣬��˵�����ɣ������䣬�����m+n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵ���![]() �У�
�У�![]() Ϊ���ߣ����߶�
Ϊ���ߣ����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ��߶�
���õ��߶�![]() ����
����![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
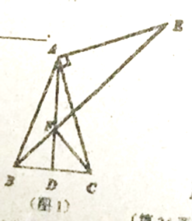
��1����![]() ����
����![]()
![]() ��
��
��2����![]() �Ƕ۽�ʱ��
�Ƕ۽�ʱ��
������ͼ2�������ⲹȫͼ�Σ��������Ӧ��ĸ��
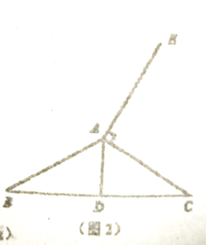
��̽��ͼ2��![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com