
观察下列各式,并回答问题
1+3=4=
1+3+5=9=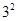
1+3+5+7=16=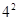
1+3+5+7+9=25=
… …
(1)请你写出第10个式子;
(2)请你用含 n 的式子表示上述式子所表述的规律;
(3)计算1+3+5+7+9…+1003+1005+…+2009+2011;
(4)计算:1005+1007+……+2009+2011。
(1)112(2)(n+1)2(3)10062(4)760032
【解析】(1)1+3+5+7+9+11+13+15+17+19+21=121=112;
(2)1+3+5+7+9+…+2n+1=(n+1)2;
(3)1+3+5+7+9…+1003+1005+…+2009+2011=10062;
(4)原式=10062﹣5022=760032.
(1)由1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…可以看出连续奇数的和等于数的个数的平方;由此可以写出第10个式子;
(2)自然数n(n≥1)表示奇数为2n+1,因此得到一般规律;
(3)根据(2)中的规律可直接计算出结果;
(4)1005+1007+…+2009+2011=(1+3+5+…+2011)﹣(1+3+5+…+1003),再用(2)中的规律计算即可.


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| (n-1)n |
| 1 |
| n(n+1) |
| 1 |
| (x-4)(x-3) |
| 1 |
| (x-3)(x-2) |
| 1 |
| (x-2)(x-1) |
| 1 |
| (x-1)x |
| 1 |
| x(x+1) |
| 1 |
| x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com