
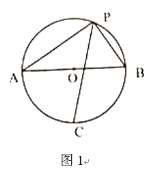
【题目】(1)已知:如图1,AB是![]() 的直径,点P为
的直径,点P为![]() 上一点(且点P不与A、B重合)连接PA,PB,
上一点(且点P不与A、B重合)连接PA,PB,![]() 的角平分线PC交
的角平分线PC交![]() 于点C.
于点C.
①若![]() ,求AB的长
,求AB的长
②求证:![]()
(2)如图2,在正方形ABCD中,![]() ,若点P满足
,若点P满足![]() ,且
,且![]() ,请直接写出点B到AP的距离.
,请直接写出点B到AP的距离.

【答案】(1)①![]() ,②见解析;(2)
,②见解析;(2)![]() 或
或![]()
【解析】
(1)①由AB是![]() 的直径,在Rt
的直径,在Rt![]() 中,利用勾股定理可求得AB的长;
中,利用勾股定理可求得AB的长;
②延长![]() 到
到![]() ,使
,使![]() ,构造
,构造![]()
![]() 和
和![]() 中,
中,
在同圆中利用圆周角相等,所对弧相等,所对的弦相等,证明![]() ,
,
利用圆内接四边形的一个外角等于不相邻的内角,证明![]() ,
,
BD=PA为所作,所以![]() (SAS)
(SAS)
从而证得:![]() ,
,
易证明![]() 是直角三角形,利用勾股定理可证明结论.
是直角三角形,利用勾股定理可证明结论.
(2)要满足![]() ,P点一定落在正方形的外接圆上,分两种情况:
,P点一定落在正方形的外接圆上,分两种情况:
P点在![]() 上或P点在
上或P点在![]() 上,
上,
在Rt![]() ABC和Rt
ABC和Rt![]() APC中,可求得AC、AP的长,
APC中,可求得AC、AP的长,
利用同圆中同弧所对圆周角相等,证得![]() ,
,
证得:Rt![]() QPB为等腰直角三角形,
QPB为等腰直角三角形,
设BQ=x,把已知和未知归结到Rt![]() QAB中,利用方程思想可以求得x的值.
QAB中,利用方程思想可以求得x的值.
(1)①![]() AB是
AB是![]() 的直径,∴
的直径,∴![]() ,
,
在Rt![]() 中,
中,![]() ,
,
∴![]() ,
,
故答案是:![]()
②如图,延长AB到D,使![]() ,连接
,连接![]()
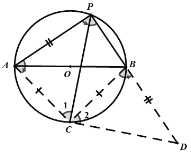
∵PC是![]() 的平分线,
的平分线,
∴![]() ,
,![]()
四边形APBC是圆内接四边形,
∴![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
∴![]() (SAS)
(SAS)
∴![]() ,
,
∵![]()
∴![]() 即
即![]()
在Rt![]() 中,
中,![]()
即:![]()
∴![]()
(2)要满足![]() ,P点一定在正方形的外接圆上,分两种情况:
,P点一定在正方形的外接圆上,分两种情况:
第一种情况,P点在![]() 上,如图:连接
上,如图:连接![]() ,作
,作![]() ,
,
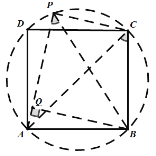
在![]() 中,
中,![]() ,∴AC=
,∴AC=![]() ,
,
在![]() 中,
中,![]() ,由勾股数可得:
,由勾股数可得:![]() ,
,
![]() ,
,
在![]() 中,
中,![]() , ∴
, ∴![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]()
即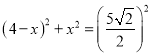 ,化简得:
,化简得:![]()
即![]() ,解得:
,解得:![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
故答案为:![]() .
.
第二种情况,P点在![]() 上,如图:
上,如图:
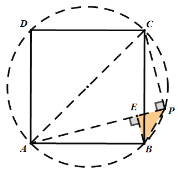
依照第一种情况得出的数据,![]()
![]()
在![]() 中,
中,![]() , ∴PE=BE,
, ∴PE=BE,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]()
即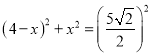 ,化简得:
,化简得:![]()
即![]() ,解得:
,解得:![]() (不合题意,舍去),
(不合题意,舍去),![]()
故答案为:![]() .
.
综上:点B到AP的距离是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家,爱园艺”、
.“爱我家,爱园艺”、![]() .“园艺小清新之旅”和
.“园艺小清新之旅”和![]() .“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
.“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李欣选择线路![]() .“园艺小清新之旅”的概率是多少?
.“园艺小清新之旅”的概率是多少?
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一线路游览的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象的对称轴是直线
的图象的对称轴是直线![]() ,则下列理论:①
,则下列理论:①![]() ,
, ![]() ②
②![]() ,③
,③![]() ,④
,④![]() ,⑤当
,⑤当![]() 时,
时, ![]() 随
随![]() 的增大而减小,其中正确的是( ).
的增大而减小,其中正确的是( ).

A. ①②③ B. ②③④ C. ③④⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
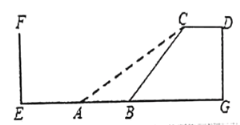
【题目】速滑运动受到许多年轻人的喜爱。如图,四边形![]() 是某速滑场馆建造的滑台,已知
是某速滑场馆建造的滑台,已知![]() ,滑台的高
,滑台的高![]() 为
为![]() 米,且坡面
米,且坡面![]() 的坡度为
的坡度为![]() .后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为
.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为![]() .
.
(1)求新坡面![]() 的坡角及
的坡角及![]() 的长;
的长;
(2)原坡面底部![]() 的正前方
的正前方![]() 米处
米处![]() 是护墙
是护墙![]() ,为保证安全,体育管理部门规定,坡面底部至少距护墙
,为保证安全,体育管理部门规定,坡面底部至少距护墙![]() 米。请问新的设计方案能否通过,试说明理由(参考数据:
米。请问新的设计方案能否通过,试说明理由(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为![]() 斜边AB上的一点,以OA为半径的
斜边AB上的一点,以OA为半径的![]() 与BC切于点D,与AC交于点E,连接AD.
与BC切于点D,与AC交于点E,连接AD.
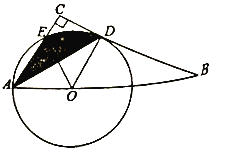
(1)求证:AD平分![]()
(2)若![]() ,
,![]() ,求阴影部分的面积.(结果保留
,求阴影部分的面积.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=9,BC=12,D是AB边的中点,P是BC边上一动点(点P不与B、C重合),若以D、C、P为顶点的三角形与△ABC相似,则线段PC=__________.
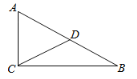
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD的顶点A、B在![]() 轴上,点A在点B的左侧,点D在
轴上,点A在点B的左侧,点D在![]() 轴的正半轴上,
轴的正半轴上,![]() ,点A的坐标为
,点A的坐标为![]() .
.
(1)求D点的坐标.
(2)求直线AC的函数关系式.
(3)动点P从点A出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.求
秒.求![]() 为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
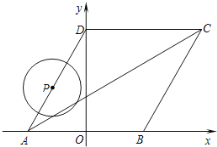
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:对于关于![]() 的函数
的函数![]() ,我们称函数
,我们称函数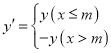 为函数y的m分函数(其中m为常数).
为函数y的m分函数(其中m为常数).
例如:对于关于x一次函数![]() 的
的![]() 分函数为
分函数为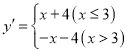
(1)若点![]() 在关于x的一次函数
在关于x的一次函数![]() 的
的![]() 分函数上,求
分函数上,求![]() 的值;
的值;
(2)写出反比例函数![]() 的
的![]() 分函数的图象上y随x的增大而减小的x的取值范围: ;
分函数的图象上y随x的增大而减小的x的取值范围: ;
(3)若![]() 是二次函数
是二次函数![]() 关于x的
关于x的![]() 分函数,
分函数,
①当![]() 时,求y的取值范围;
时,求y的取值范围;
②当![]() 时,
时,![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
③若点![]() ,连结
,连结![]() ,当关于
,当关于![]() 的二次函数
的二次函数![]() 的
的![]() 分函数,与线段MN有两个交点,直接写出m的取值范围.
分函数,与线段MN有两个交点,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com