
ЁОЬтФПЁПаТЖЈвхЃКЖдгкЙигк![]() ЕФКЏЪ§
ЕФКЏЪ§![]() ЃЌЮвУЧГЦКЏЪ§
ЃЌЮвУЧГЦКЏЪ§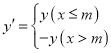 ЮЊКЏЪ§yЕФmЗжКЏЪ§ЃЈЦфжаmЮЊГЃЪ§ЃЉ.
ЮЊКЏЪ§yЕФmЗжКЏЪ§ЃЈЦфжаmЮЊГЃЪ§ЃЉ.
Р§ШчЃКЖдгкЙигкxвЛДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЮЊ
ЗжКЏЪ§ЮЊ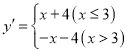
ЃЈ1ЃЉШєЕу![]() дкЙигкxЕФвЛДЮКЏЪ§
дкЙигкxЕФвЛДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЩЯЃЌЧѓ
ЗжКЏЪ§ЩЯЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉаДГіЗДБШР§КЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЕФЭМЯѓЩЯyЫцxЕФдіДѓЖјМѕаЁЕФxЕФШЁжЕЗЖЮЇЃК ЃЛ
ЗжКЏЪ§ЕФЭМЯѓЩЯyЫцxЕФдіДѓЖјМѕаЁЕФxЕФШЁжЕЗЖЮЇЃК ЃЛ
ЃЈ3ЃЉШє![]() ЪЧЖўДЮКЏЪ§
ЪЧЖўДЮКЏЪ§![]() ЙигкxЕФ
ЙигкxЕФ![]() ЗжКЏЪ§ЃЌ
ЗжКЏЪ§ЃЌ
ЂйЕБ![]() ЪБЃЌЧѓyЕФШЁжЕЗЖЮЇЃЛ
ЪБЃЌЧѓyЕФШЁжЕЗЖЮЇЃЛ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФШЁжЕЗЖЮЇЮЊ ЃЛ
ЕФШЁжЕЗЖЮЇЮЊ ЃЛ
ЂлШєЕу![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌЕБЙигк
ЃЌЕБЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇ.
ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЌжБНгаДГіmЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉn=3ЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉЂй
ЃЛЃЈ3ЃЉЂй![]() Лђ
Лђ![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂлmЃМ
ЃЛЂлmЃМ![]() Лђ
Лђ![]() ЁмmЃМ
ЁмmЃМ![]() Лђ
Лђ![]() Ёмm.
Ёмm.
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШаДГівЛДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌШЛКѓНЋЕуPДњШыМДПЩЧѓГіnЃЛ
ЗжКЏЪ§ЃЌШЛКѓНЋЕуPДњШыМДПЩЧѓГіnЃЛ
ЃЈ2ЃЉЪзЯШаДГіЗДБШР§КЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌШЛКѓИљОнЗДБШР§КЏЪ§ЕФдіМѕадНјааХаЖЈЃЛ
ЗжКЏЪ§ЃЌШЛКѓИљОнЗДБШР§КЏЪ§ЕФдіМѕадНјааХаЖЈЃЛ
ЃЈ3ЃЉЂйЪзЯШаДГіЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌШЛКѓИљОнxЕФШЁжЕЗЖЮЇНсКЯЖўДЮКЏЪ§ЕФаджЪЗжБ№ЧѓГіЖдгІЕФyЕФШЁжЕЗЖЮЇМДПЩЃЛ
ЗжКЏЪ§ЃЌШЛКѓИљОнxЕФШЁжЕЗЖЮЇНсКЯЖўДЮКЏЪ§ЕФаджЪЗжБ№ЧѓГіЖдгІЕФyЕФШЁжЕЗЖЮЇМДПЩЃЛ
ЂкЪзЯШЧѓГіЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌШЛКѓИљОн
ЃЌШЛКѓИљОн![]() ПЩжЊЃЌЧѓГі
ПЩжЊЃЌЧѓГі![]() ЪБ
ЪБ![]() ЕФжЕдк-3КЭ-4жЎМфЃЈАќКЌ-3КЭ-4ЃЉЖдгІЕФxЕФШЁжЕЗЖЮЇМДПЩЃЛ
ЕФжЕдк-3КЭ-4жЎМфЃЈАќКЌ-3КЭ-4ЃЉЖдгІЕФxЕФШЁжЕЗЖЮЇМДПЩЃЛ
ЂлЛГі![]() КЭ
КЭ![]() ЕФКЏЪ§ЭМЯёЃЌЧѓГіСНКЏЪ§ЭМЯѓгыy=1ЕФНЛЕуЕФКсзјБъЃЌШЛКѓНсКЯКЏЪ§ЭМЯѓЗжРрЬжТлЃЌЗжБ№ЧѓГідкВЛЭЌЕФЗЖЮЇФкгыЯпЖЮMNЕФНЛЕуИіЪ§ЃЌМДПЩЕУЕНЗћКЯЬтвтЕФmЕФШЁжЕЗЖЮЇ.
ЕФКЏЪ§ЭМЯёЃЌЧѓГіСНКЏЪ§ЭМЯѓгыy=1ЕФНЛЕуЕФКсзјБъЃЌШЛКѓНсКЯКЏЪ§ЭМЯѓЗжРрЬжТлЃЌЗжБ№ЧѓГідкВЛЭЌЕФЗЖЮЇФкгыЯпЖЮMNЕФНЛЕуИіЪ§ЃЌМДПЩЕУЕНЗћКЯЬтвтЕФmЕФШЁжЕЗЖЮЇ.
НтЃКЃЈ1ЃЉгЩЬтвтЕУЃК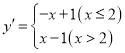 ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрАб![]() ДњШы
ДњШы![]() ЕУ
ЕУ![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩЬтвтЕУЃК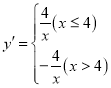 ЃЌ
ЃЌ
ИљОнКЏЪ§НтЮіЪНПЩжЊЃЌЕБ![]() Лђ
Лђ![]() ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛ
ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛ
ЃЈ3ЃЉЂйгЩЬтвтЕУЃК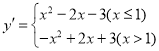 ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФЭМЯѓyЫцxЕФдіДѓЖјМѕаЁЃЌ
ЕФЭМЯѓyЫцxЕФдіДѓЖјМѕаЁЃЌ
Аб![]() ДњШы
ДњШы![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ
Аб![]() ДњШы
ДњШы![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФЭМЯѓyЫцxЕФдіДѓЖјМѕаЁЃЌ
ЕФЭМЯѓyЫцxЕФдіДѓЖјМѕаЁЃЌ
Аб![]() ДњШы
ДњШы![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ
Аб![]() ДњШы
ДњШы![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ
злЩЯЃЌ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЂкЁпАб![]() ДњШы
ДњШы![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ
Аб![]() ДњШы
ДњШы![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЛ
ЃЛ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЌ
ЃЌ
гЩЂйжЊЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
АбyЃНЃ3ДњШы![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЈИКжЕвбЩсШЅЃЉЃЌ
ЃЈИКжЕвбЩсШЅЃЉЃЌ
АбyЃНЃ4ДњШы![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЈИКжЕвбЩсШЅЃЉЃЌ
ЃЈИКжЕвбЩсШЅЃЉЃЌ
Ёр![]() ЕФШЁжЕЗЖЮЇЮЊ
ЕФШЁжЕЗЖЮЇЮЊ![]() ЃЛ
ЃЛ
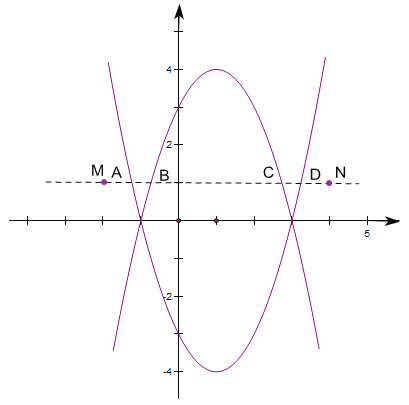
ЂлШчЭМЮЊ![]() КЭ
КЭ![]() ЕФКЏЪ§ЭМЯёЃЌAЁЂBЁЂCЁЂDЗжБ№ЪЧСНКЏЪ§ЭМЯѓгыy=1ЕФНЛЕуЃЌ
ЕФКЏЪ§ЭМЯёЃЌAЁЂBЁЂCЁЂDЗжБ№ЪЧСНКЏЪ§ЭМЯѓгыy=1ЕФНЛЕуЃЌ
СЊСЂ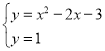 ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрAЕуКсзјБъЮЊ![]() ЃЌDЕуКсзјБъЮЊ
ЃЌDЕуКсзјБъЮЊ![]() ЃЌ
ЃЌ
СЊСЂ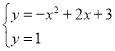 ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрBЕуКсзјБъЮЊ![]() ЃЌCЕуКсзјБъЮЊ
ЃЌCЕуКсзјБъЮЊ![]() ЃЌ
ЃЌ
НсКЯКЏЪ§ЭМЯѓЃЌЗжРрЬжТлЃК
ЂйЕБmЃМ![]() ЪБЃЌЙигк
ЪБЃЌЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЛ
ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЛ
ЂкЕБ![]() ЁмmЃМ
ЁмmЃМ![]() ЪБЃЌЙигк
ЪБЃЌЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌгыЯпЖЮMNгаШ§ИіНЛЕуЃЛ
ЗжКЏЪ§ЃЌгыЯпЖЮMNгаШ§ИіНЛЕуЃЛ
ЂлЕБ![]() ЁмmЃМ
ЁмmЃМ![]() ЪБЃЌЙигк
ЪБЃЌЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЛ
ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЛ
Ђм![]() ЁмmЃМ
ЁмmЃМ![]() ЪБЃЌЙигк
ЪБЃЌЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌгыЯпЖЮMNгавЛИіНЛЕуЃЛ
ЗжКЏЪ§ЃЌгыЯпЖЮMNгавЛИіНЛЕуЃЛ
ЂнЕБ![]() ЁмmЪБЃЌЙигк
ЁмmЪБЃЌЙигк![]() ЕФЖўДЮКЏЪ§
ЕФЖўДЮКЏЪ§![]() ЕФ
ЕФ![]() ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЛ
ЗжКЏЪ§ЃЌгыЯпЖЮMNгаСНИіНЛЕуЃЛ
злЩЯЫљЪіЃКmЕФШЁжЕЗЖЮЇЪЧmЃМ![]() Лђ
Лђ![]() ЁмmЃМ
ЁмmЃМ![]() Лђ
Лђ![]() Ёмm.
Ёмm.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
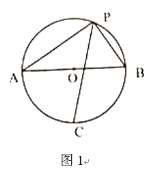
ЁОЬтФПЁПЃЈ1ЃЉвбжЊЃКШчЭМ1ЃЌABЪЧ![]() ЕФжБОЖЃЌЕуPЮЊ
ЕФжБОЖЃЌЕуPЮЊ![]() ЩЯвЛЕуЃЈЧвЕуPВЛгыAЁЂBжиКЯЃЉСЌНгPAЃЌPBЃЌ
ЩЯвЛЕуЃЈЧвЕуPВЛгыAЁЂBжиКЯЃЉСЌНгPAЃЌPBЃЌ![]() ЕФНЧЦНЗжЯпPCНЛ
ЕФНЧЦНЗжЯпPCНЛ![]() гкЕуC.
гкЕуC.
ЂйШє![]() ЃЌЧѓABЕФГЄ
ЃЌЧѓABЕФГЄ
ЂкЧѓжЄЃК![]()
ЃЈ2ЃЉШчЭМ2ЃЌдке§ЗНаЮABCDжаЃЌ![]() ЃЌШєЕуPТњзу
ЃЌШєЕуPТњзу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧыжБНгаДГіЕуBЕНAPЕФОрРы.
ЃЌЧыжБНгаДГіЕуBЕНAPЕФОрРы.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
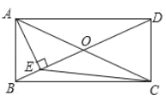
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЁЂ
ЁЂ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЕФУцЛ§ЪЧЃЈ ЃЉ
ЕФУцЛ§ЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЛњаЕЙЋЫООЯњвЛжжСуМўЃЌвбжЊетжжСуМўЕФГЩБОЮЊУПМў20дЊЃЌЕїВщЗЂЯжЕБЯњЪлМлЮЊ24дЊЃЌЦНОљУПЬьФмЪлГі32МўЃЌЖјЕБЯњЪлМлУПЩЯеЧ2дЊЃЌЦНОљУПЬьОЭЩйЪлГі4Мў.
(1)ШєЙЋЫОУПЬьЕФЯњЪлМлЮЊxдЊЃЌдђУПЬьЕФЯњЪлСПЮЊЖрЩй?
(2)ШчЙћЮяМлВПУХЙцЖЈетжжСуМўЕФЯњЪлМлВЛЕУИпгкУПМў28дЊЃЌИУЙЋЫОЯывЊУПЬьЛёЕУ150дЊЕФЯњЪлРћШѓЃЌЯњЪлМлгІЕБЮЊЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮ![]() жаЃЌЕу
жаЃЌЕу![]() КЭЕу
КЭЕу![]() ЪЧЖдНЧЯп
ЪЧЖдНЧЯп![]() ЩЯЕФСНЕуЃЌ
ЩЯЕФСНЕуЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() ЕФбгГЄЯпЕу
ЕФбгГЄЯпЕу![]() .
.
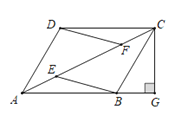
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФУцЛ§ЪЧ .
ЕФУцЛ§ЪЧ .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
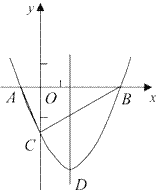
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=![]() x2+bxЃ2гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЧвAЃЈвЛ1ЃЌ0ЃЉЃЎ
x2+bxЃ2гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЧвAЃЈвЛ1ЃЌ0ЃЉЃЎ
ЂХЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕуDЕФзјБъЃЛ
ЂЦХаЖЯЁїABCЕФаЮзДЃЌжЄУїФуЕФНсТлЃЛ
ЂЧЕуM(mЃЌ0)ЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЕБCM+DMЕФжЕзюаЁЪБЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕ![]() жаЕФЖЏЕу
жаЕФЖЏЕу![]() КЭЭМаЮ
КЭЭМаЮ![]() ЃЌИјГіШчЯТЖЈвхЃКШчЙћ
ЃЌИјГіШчЯТЖЈвхЃКШчЙћ![]() ЮЊЭМаЮ
ЮЊЭМаЮ![]() ЩЯвЛИіЖЏЕуЃЌ
ЩЯвЛИіЖЏЕуЃЌ![]() ЃЌ
ЃЌ![]() СНЕуМфОрРыЕФзюДѓжЕЮЊ
СНЕуМфОрРыЕФзюДѓжЕЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() СНЕуМфОрРыЕФзюаЁжЕЮЊ
СНЕуМфОрРыЕФзюаЁжЕЮЊ![]() ЃЌЮвУЧАб
ЃЌЮвУЧАб![]() ЕФжЕНаЕу
ЕФжЕНаЕу![]() КЭЭМаЮ
КЭЭМаЮ![]() МфЕФЁАКЭОрРыЁБЃЌМЧзї
МфЕФЁАКЭОрРыЁБЃЌМЧзї![]() ЃЈ
ЃЈ![]() ЃЌЭМаЮ
ЃЌЭМаЮ![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉШчЭМЃЌе§ЗНаЮ![]() ЕФжааФЮЊЕу
ЕФжааФЮЊЕу![]() ЃЌ
ЃЌ![]() .
.
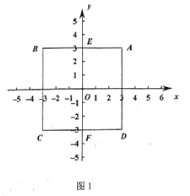
ЂйЕу![]() ЕНЯпЖЮ
ЕНЯпЖЮ![]() ЕФЁАКЭОрРыЁБ
ЕФЁАКЭОрРыЁБ![]() ЃЈ
ЃЈ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЃЉ=______ЃЛ
ЃЉ=______ЃЛ
ЂкЩшИУе§ЗНаЮгы![]() жсНЛгкЕу
жсНЛгкЕу![]() КЭ
КЭ![]() ЃЌЕу
ЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЈ
ЃЈ![]() ЃЌе§ЗНаЮ
ЃЌе§ЗНаЮ![]() ЃЉ=7ЃЌЧѓЕу
ЃЉ=7ЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
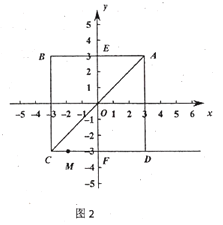
ЃЈ2ЃЉШчЭМ2ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЙ§![]() ЃЌ
ЃЌ![]() СНЕузїЩфЯп
СНЕузїЩфЯп![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕу
ЃЌЕу![]() ЪЧЩфЯп
ЪЧЩфЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌШчЙћ
ЩЯЕФвЛИіЖЏЕуЃЌШчЙћ![]() ЃЈ
ЃЈ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЃЉ
ЃЉ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕуКсзјБъ
ЕуКсзјБъ![]() ШЁжЕЗЖЮЇ.
ШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌШєPКЭQСНЕуЙигкдЕуЖдГЦЃЌдђГЦЕуPгыЕуQЪЧвЛИіЁАКЭаГЕуЖдЁБЃЌБэЪОЮЊ[PЃЌQ]ЃЌБШШч[PЃЈ1ЃЌ2ЃЉЃЌQЃЈЉ1ЃЌЉ2ЃЉ]ЪЧвЛИіЁАКЭаГЕуЖдЁБЃЎ
ЃЈ1ЃЉаДГіЗДБШР§КЏЪ§yЃН![]() ЭМЯѓЩЯЕФвЛИіЁАКЭаГЕуЖдЁБЃЛ
ЭМЯѓЩЯЕФвЛИіЁАКЭаГЕуЖдЁБЃЛ
ЃЈ2ЃЉвбжЊЖўДЮКЏЪ§yЃНx2+mx+nЃЌ
ЂйШєДЫКЏЪ§ЭМЯѓЩЯДцдквЛИіКЭаГЕуЖд[AЃЌB]ЃЌЦфжаЕуAЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЌЧѓmЃЌnЕФжЕЃЛ
ЂкдкЂйЕФЬѕМўЯТЃЌдкyжсЩЯШЁвЛЕуMЃЈ0ЃЌbЃЉЃЌЕБЁЯAMBЮЊШёНЧЪБЃЌЧѓbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭђжнЖўжаАЫЪЎжмФъаЃЧьРДСйжЎМЪЃЌбЇаЃБОзХЁАМђЦгЃЌНкМѓЃЌЪЕаЇЃЌЬиЩЋЁБЕФддђНЋ 2019Фъ 10 дТ 25 ШежС 11 дТ 25 ШеЖЈЮЊаЃгбЛиЗУдТЃЌбЇаЃзмЮёДІЙКТђСЫКьЃЌЛЦЃЌРЖШ§жжЛЈЛмзААч Гі AЃЌBЃЌCЃЌD ЫФжждьаЭЃЌЦфжавЛИі A дьаЭашвЊ 15 ХшКьЛЈЃЌ10 ХшЛЦЛЈЃЌ10 ХшРЖЛЈЃЛвЛИі B дьаЭашвЊ 5 ХшКьЛЈЃЌ7 ХшЛЦЛЈЃЌ6 ХшРЖЛЈЃЛвЛИі C дьаЭашвЊ 7 ХшКьЛЈЃЌ8 ХшЛЦЛЈЃЌ9 ХшРЖ ЛЈЃЛвЛИі D дьаЭашвЊ 7 ХшКьЛЈЃЌ10 ХшЛЦЛЈЃЌ10 ХшРЖЛЈЃЌШєвЛИі A дьаЭЪлМл 1800 дЊЃЌРћШѓ ТЪЮЊ 20%ЃЌвЛИі B КЭвЛИі C дьаЭвЛЙВГЩБОКЭЮЊ 1935 дЊЃЌЧввЛХшКьЛЈЕФРћШѓТЪЮЊ 25%ЃЌдђвЛИі D дьаЭЕФЪлМлЮЊ_____дЊЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com