
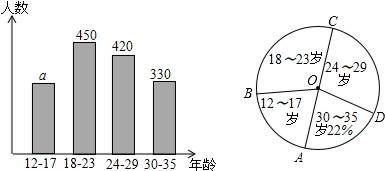
分析 (1)由AC为圆的直径可知:a+450=420+330,从而可求得a的值;
(2)扇形圆心角的大小=360°×百分比;
(3)先求得18至29岁人数所占的百分比,然后根据频数=总数×百分比,即可求得年龄在18〜29岁的人数.
解答 解:(1)a+450=420+330,a=300(人)
被调查的人数=300+450+420+330=1500(人);
(2)${360°}×\frac{330}{1500}×100%={79.2°}$;
(3)∵12~35岁网瘾人数约为2000万,
∴18~29岁的人数约为2000万×$\frac{450+420}{1500}$=1160(万).
点评 本题主要考查的是条形统计图和扇形统计图,明确频数、百分比、数据总数之间的关系是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 某校为了解学生喜爱的体育活动项目情况,随机抽查了若干名学生,让每人选一项自己最喜欢的项目,并制成如图所示的扇形统计图.如果该校有900名学生,则喜爱跳绳的学生约有270人.
某校为了解学生喜爱的体育活动项目情况,随机抽查了若干名学生,让每人选一项自己最喜欢的项目,并制成如图所示的扇形统计图.如果该校有900名学生,则喜爱跳绳的学生约有270人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
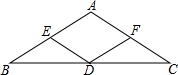 如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.
如图,已知△ABC中,AB=AC,E,D,F分别是边AB,BC,AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.69分 | B. | 9.70分 | C. | 9.71分 | D. | 9.72分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com