
【题目】如图1,在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() .
.
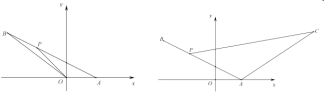
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)点![]() 是线段
是线段![]() 上的一点,当
上的一点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
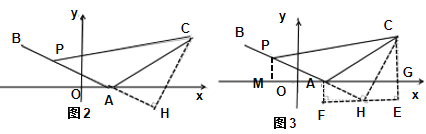
(3)如图2,在(2)的条件下,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 落在点
落在点![]() 处,连结
处,连结![]() ,求
,求![]() 的面积,并直接写出点
的面积,并直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,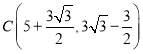 .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)过点![]() 、
、![]() 分别做
分别做![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,根据相似三角形的性质得出PM的长,即点P的纵坐标,代入直线解析式,从而求解;
,根据相似三角形的性质得出PM的长,即点P的纵坐标,代入直线解析式,从而求解;
(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若求
,若求![]() 的面积,求出CH的长即可,根据旋转120°,得∠CAH=60°,解直角三角形AHC即可得出CH长,从而求解,
的面积,求出CH的长即可,根据旋转120°,得∠CAH=60°,解直角三角形AHC即可得出CH长,从而求解,
解:(1) )∵A(2,0),![]() ,
,
设直线AB的解析式为y=kx+b,则有![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为![]() .
.
(2)如图1,过点![]() 、
、![]() 分别做
分别做![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,即PM∥BN.
,即PM∥BN.
∵![]() ,
,
∴AP:AB=2:3,
∴![]() =
=![]()
∴![]()
将![]() 代入解析式
代入解析式![]() 可得
可得
![]() ,∴
,∴![]()
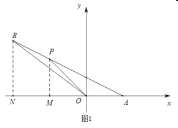
(3)①如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
∵![]() 中,由勾股定理得:AP=
中,由勾股定理得:AP=![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]() ;
;
②过点H作FE∥x轴,过点C作CE⊥FE于点E,交x轴于点G,过点A作AF⊥FE于点F,
Rt△ACH中, AH=![]() ,
,
∵PM∥AF,AM∥HF,根据直角相等、两直线平行,同位角相等易证△APM∽△HAF,AP=2![]() ,AM=4,PM=2,
,AM=4,PM=2,
∴![]() ,即
,即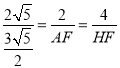 ,
,
解得:AF=![]() ,HF=3,
,HF=3,
∵∠AHF+∠CHE=∠AHF +∠FAH=90°,
∴∠CHE=∠FAH,
∵∠HEC=∠AFH=90°,
∴△HEC∽△AFH,
方法同上得:CE=3![]() ,HE=
,HE=![]() ,
,
由四边形AFEG是矩形,得AF=GE= ![]() ,AG=FH+HE,
,AG=FH+HE,
∴OG=OA+ FH+HE=2+3+![]() =5+
=5+![]() ,CG=CE-EG=3
,CG=CE-EG=3![]() -
-![]() ,
,
即点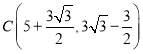 .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 为圆心作⊙
为圆心作⊙![]() ,⊙
,⊙![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 为⊙
为⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,连接
的任意一点,连接![]() 、
、![]() ,过
,过![]() 点分别作
点分别作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() .当
.当![]() 点在⊙
点在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
运动到点![]() 的过程中,下列图象中能表示
的过程中,下列图象中能表示![]() 与
与![]() 的函数关系的部分图象是( )
的函数关系的部分图象是( )

A.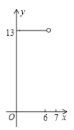 B.
B.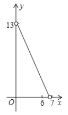 C.
C.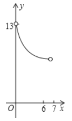 D.
D.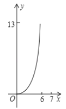
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月进馆达到288人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不得超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接待第四个月的进馆人次,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有2个红球和2个白球,这些球除颜色外其余都相同,先从袋中摸出1个球后不放回,再摸出一个球.
(1)请用树状图或列表法列举出两次摸球可能出现的各种结果.
(2)求两次摸到不同颜色的球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某小区青年对“高铁”、“扫码支付”、“网购”和“共享单车”新四大发明的喜爱程度,随机调查该小区一部分青年(每名青年只能选一个),并将调查结果制成如图所示统计表与条形统计图.
青年最喜爱的新四大发明人数统计表
节目 | 人数(名) | 百分比 |
共享单车 | 5 |
|
扫码支付 | 15 |
|
网购 |
|
|
高铁 | 10 |
|
青年最喜爱的新四大发明人数条形统计图
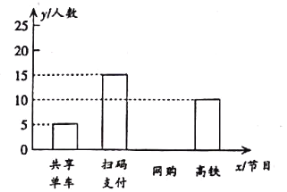
(1)计算![]() 的值
的值![]() ;
;
(2)请补全条形统计图;
(3)在被调查喜爱“共享单车”青年中,小明一周内使用共享单车的次数分别为:1,3,5,12,![]() ,若整数
,若整数![]() 是这组数据的中位数,直接写出该组数据的平均数.
是这组数据的中位数,直接写出该组数据的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具公司生产一种电子玩具,每只玩具的生产成本为18元,试销过程中发现,每月销售量y(万只)与销售单价x(元)之间的关系可以近似的看作一次函数y=2x+100,设每月销售这种玩具的利润为w(万元).
(1)写出w与x之间的函数表达式;
(2)当销售单价为多少元时,公司每月获得的利润为440万元?
(3)如果公司每月的生产成本不超过540万元,那么当销售单价为多少元时,公司每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm,AD=2cm,动点M自点A出发沿A→B的方向,以每秒1cm的速度运动,同时动点N自点A出发沿A→D→C的方向以每秒2cm的速度运动,当点N到达点C时,两点同时停止运动,设运动时间为x(秒),△AMN的面积为y(cm2),则下列图象中能反映y与x之间的函数关系的是( )
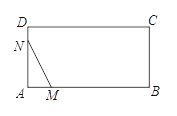
A.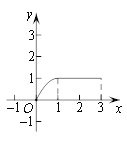 B.
B.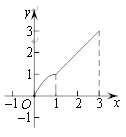 C.
C.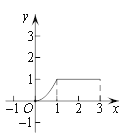 D.
D.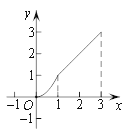
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com