
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将ΔADP沿AP翻折得到![]() ,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
图1
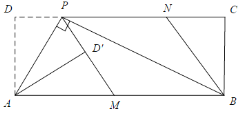
图2
(1)求证:![]() ;
;
(2)请判断四边形PMBN的形状,并说明理由;
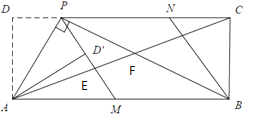
(3)如图2,连接AC,分别交PM,PB于点E,F.若tan∠PAD=![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)是菱形;(3)![]()
【解析】
(1)要证明![]() ,就需证明
,就需证明![]() =
=![]() ,根据矩形ABCD可知AD=BC,
,根据矩形ABCD可知AD=BC,
因此需要证明![]() =
=![]() ,即需要证明△ADP∽△PCB相似,
,即需要证明△ADP∽△PCB相似,
根据矩形![]() 可知
可知![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
再由![]() ,
,![]() 可知,
可知,![]() ,从而得到
,从而得到![]() ,
,
即可以根据“两角相等的两个三角形相似”来证明![]() 和
和![]() 相似。
相似。
(2)观察图形可发现四边形![]() 是菱形,
是菱形,
根据“一组邻边相等的平行四边形是菱形”可知,需要先证明四边形![]() 是平行四边形,再证明其中一组邻边相等,由
是平行四边形,再证明其中一组邻边相等,由![]() ,
,![]() ,根据“两组对边分别平行的四边形是平行四边形”即可证明四边形
,根据“两组对边分别平行的四边形是平行四边形”即可证明四边形![]() 是平行四边形,
是平行四边形,
由翻折形成的两个全等三角形![]() 和
和![]() 得出
得出![]() ,
,
进而根据![]() ,
,![]() ,得出
,得出![]() ,
,
再由![]() ,得到内错角
,得到内错角![]() 相等,等量代换为
相等,等量代换为![]() ,
,
根据“等角对等边”得出邻边![]() 和
和![]() 相等,从而说明四边形
相等,从而说明四边形![]() 是菱形。
是菱形。
(1)证明:∵![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 。
。
(2)四边形![]() 是菱形。
是菱形。
证明:因为![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() (翻折),
(翻折),
∴![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
于是![]() ,
,
∴![]() ,
,
又∵四边形![]() 是平行四边形,
是平行四边形,
∴四边形![]() 是菱形。
是菱形。
(3)(3)设![]() (
(![]() ),
),
∵在Rt△APDA中,tan∠PAD=![]()
∴![]() ,所以
,所以![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
∵![]() (翻折),
(翻折),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
于是![]() ,
,
∴![]() ,
,
∵![]() ,
,
所以![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,即CF=
,即CF=![]() AC
AC
∵![]() ,
,![]() (对顶角),
(对顶角),
∴![]() ,
,
∴![]() ,
,
∴![]() ,即AE=
,即AE=![]() AC
AC
∴![]() =
=![]() =
=![]() .
.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
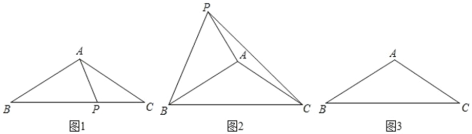
【题目】等腰△ABC 中,AB=AC,∠BAC=120°,点 P 为平面内一点.
(1)如图 1,当点 P 在边 BC 上时,且满足∠APC=120°,求![]() 的值;
的值;
(2)如图 2,当点 P 在△ABC 的外部,且满足∠APC+∠BPC=90°,求证:BP=![]() AP;
AP;
(3)如图 3,点 P 满足∠APC=60°,连接 BP,若 AP=1,PC=3,直接写出BP 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
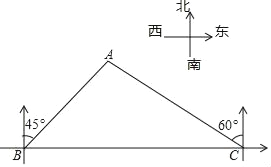
【题目】如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
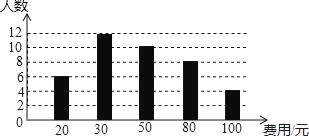
【题目】在全民读书月活动中,某校随机调查了部分同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题.
(1)这次调查获取的样本容量是 .(直接写出结果)
(2)这次调查获取的样本数据的众数是 ,中位数是 .(直接写出结果)
(3)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
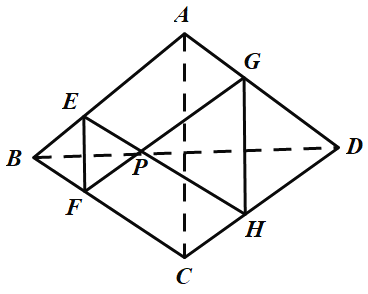
【题目】如图,菱形纸片![]() 的边长为
的边长为![]() 翻折
翻折![]() 使点
使点![]() 两点重合在对角线
两点重合在对角线![]() 上一点
上一点![]() 分别是折痕.设
分别是折痕.设![]() .
.
(1)证明:![]() ;
;
(2)当![]() 时,六边形
时,六边形![]() 周长的值是否会发生改变,请说明理由;
周长的值是否会发生改变,请说明理由;
(3)当![]() 时,六边形
时,六边形![]() 的面积可能等于
的面积可能等于![]() 吗?如果能,求此时
吗?如果能,求此时![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
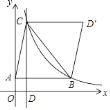
【题目】如图,在△ABC中,B、C两点恰好在反比例函数y= ![]() (k>0)第一象限的图象上,且BC=
(k>0)第一象限的图象上,且BC= ![]() ,S△ABC=
,S△ABC= ![]() ,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为________.
,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com