
【题目】如图,菱形纸片![]() 的边长为
的边长为![]() 翻折
翻折![]() 使点
使点![]() 两点重合在对角线
两点重合在对角线![]() 上一点
上一点![]() 分别是折痕.设
分别是折痕.设![]() .
.
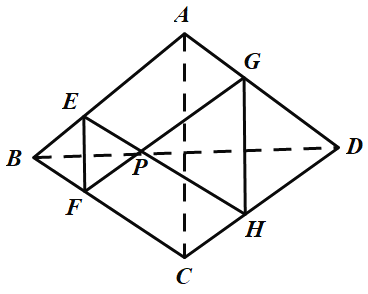
(1)证明:![]() ;
;
(2)当![]() 时,六边形
时,六边形![]() 周长的值是否会发生改变,请说明理由;
周长的值是否会发生改变,请说明理由;
(3)当![]() 时,六边形
时,六边形![]() 的面积可能等于
的面积可能等于![]() 吗?如果能,求此时
吗?如果能,求此时![]() 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
【答案】(1)见解析;(2)不变,见解析;(3)能,![]() 或
或![]()
【解析】
(1)由折叠的性质得到BE=EP,BF=PF,得到BE=BF,根据菱形的性质得到AB∥CD∥FG,BC∥EH∥AD,于是得到结论;
(2)由菱形的性质得到BE=BF,AE=FC,推出△ABC是等边三角形,求得∠B=∠D=60°,得到∠B=∠D=60°,于是得到结论;
(3)记AC与BD交于点O,得到∠ABD=30°,解直角三角形得到AO=1,BO=![]() ,求得S四边形ABCD=2
,求得S四边形ABCD=2![]() ,当六边形AEFCHG的面积等于
,当六边形AEFCHG的面积等于![]() 时,得到S△BEF+S△DGH=
时,得到S△BEF+S△DGH=![]() ,设GH与BD交于点M,求得GM=
,设GH与BD交于点M,求得GM=![]() x,根据三角形的面积列方程即可得到结论.
x,根据三角形的面积列方程即可得到结论.
解:![]() 折叠后
折叠后![]() 落在
落在![]() 上,
上,
![]()
![]()
![]() 平分
平分![]()
![]() ,
,
![]() 四边形
四边形![]() 为菱形,同理四边形
为菱形,同理四边形![]() 为菱形,
为菱形,
![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() .
.
![]() 不变.
不变.
理由如下:由![]() 得
得![]()
![]() 四边形
四边形![]() 为菱形,
为菱形,
![]()
![]() 为等边三角
为等边三角
![]() ,
,
![]()
![]() 为定值.
为定值.
![]() 记
记![]() 与
与![]() 交于点
交于点![]() .
.

![]()
![]()
![]()
![]()
![]()
![]()
当六边形![]() 的面积为
的面积为![]() 时,
时,
![]()
由![]() 得
得![]()
![]()
![]()
![]()
记![]() 与
与![]() 交于点
交于点![]()

![]() ,
,![]()
![]()
同理![]()
即![]()
化简得![]()
解得![]() ,
,![]()
∴当![]() 或
或![]() 时,六边形
时,六边形![]() 的面积为
的面积为![]() .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】现有两个不透明的乒乓球盒,甲盒中装有1个白球和2个红球,乙盒中装有2个白球和若干个红球,这些小球除颜色不同外,其余均相同.若从乙盒中随机摸出一个球,摸到红球的概率为![]() .
.
(1)求乙盒中红球的个数;
(2)若先从甲盒中随机摸出一个球,再从乙盒中随机摸出一个球,请用树形图或列表法求两次摸到不同颜色的球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将ΔADP沿AP翻折得到![]() ,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
图1
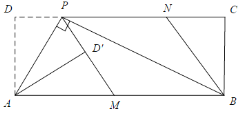
图2
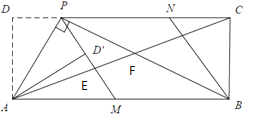
(1)求证:![]() ;
;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若tan∠PAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() ,
,![]() 为对角线
为对角线![]() 上的一点,连接
上的一点,连接![]() 和
和![]() .
.
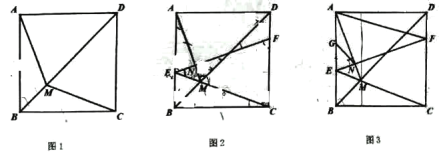
(1)求证:![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点,且有
于点,且有![]() .
.
①判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
②如图3,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,当四边形
,当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为 _________ .
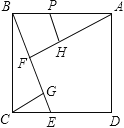
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C; ②∠AEF=∠AFE; ③∠EBC=∠C;④AG⊥EF.正确结论有( )
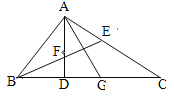
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com