
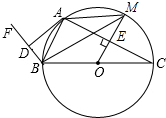
 如图,已知BC为⊙O的直径,BA平分∠FBC交⊙O于点A,D是射线BF上的一点,且满足$\frac{BD}{BA}$=$\frac{BA}{BC}$,过点O作OM⊥AC于点E,交⊙O于点M,连接BM,AM.
如图,已知BC为⊙O的直径,BA平分∠FBC交⊙O于点A,D是射线BF上的一点,且满足$\frac{BD}{BA}$=$\frac{BA}{BC}$,过点O作OM⊥AC于点E,交⊙O于点M,连接BM,AM.分析 (1)要证AD是⊙O的切线,连接OA,只证∠DAO=90°即可.
(2)连接CM,根据垂径定理求得$\widehat{MC}$=$\widehat{MA}$,进而求得∠ABM=∠CBM,AM=CM=6,从而得出sin∠CBM=$\frac{3}{5}$,在RT△BMC中,利用正弦函数即可求得直径AB,进而求得半径.
解答 (1)证明:连接OA;
∵BA平分∠CBF,
∴∠ABD=∠CBA,
∵$\frac{BD}{BA}=\frac{BA}{BC}$,
∴△ADB∽△CBA,
∴∠ADB=∠CAB,
又∵BC为⊙O的直径,
∴∠CAB=90°,∠ADB=90°,
又∵点A在圆O上,
∴OA=OB,∠OAB=∠OBA=∠DBA,
∴FB∥OA,
∴∠ADB+∠OAD=180°,
∠OAD=90°,
∴OA⊥DA,∵OA为半径,
∴DA为⊙O的切线.
(2)解:连接CM,
∵OM⊥AC于点E,OM是半径,
∴$\widehat{MC}$=$\widehat{MA}$,
∴∠ABM=∠CBM,AM=CM=6,
∴sin∠ABM=sin∠CBM=$\frac{3}{5}$,
∵BC为⊙O的直径,
∴∠BMC=90°,
在RT△BMC中,sin∠CBM=$\frac{3}{5}$,
∴$\frac{MC}{BC}$=$\frac{3}{5}$,
∴BC=10,
∴⊙O的半径为5.
点评 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了三角函数的知识.


科目:初中数学 来源: 题型:解答题
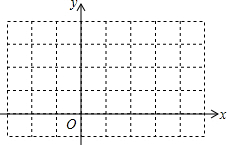 (1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;
(1)根据画函数图象的步骤,在如图的直角坐标系中,画出函数y=|x|的图象;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
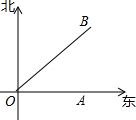 台风中线位于O处洋面上,以40km/h的速度向东北方向移动,在半径为240km的范围内受台风的影响,城市A位于O处的正东方向320km处,问A市是否会遭受此台风的影响?若受影响,求影响时间;若不受影响,请说明理由.(精确到个位)
台风中线位于O处洋面上,以40km/h的速度向东北方向移动,在半径为240km的范围内受台风的影响,城市A位于O处的正东方向320km处,问A市是否会遭受此台风的影响?若受影响,求影响时间;若不受影响,请说明理由.(精确到个位)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2
如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )
如图,在半径为2,圆心角为90°的扇形内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为( )| A. | π-1 | B. | 2π-1 | C. | $\frac{1}{2}$π-1 | D. | $\frac{1}{2}$π-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
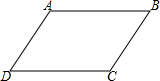 (1)∵∠A+∠B=180°(已知)
(1)∵∠A+∠B=180°(已知)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com