
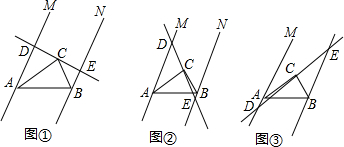
分析 (1)如图①在AB上截取AG=AD,连接CG,利用三角形全等的判定定理可判断出BG=BE,即AD+BE=AB;
(2)如图②,可以在AD上截取线段等于AB,如图③,可在BE上截取线段等于AB,仿照(1)的证明方法来证明;
(3)本问题如图①,高AB边上的高为hAB,利用面积公式可求得.
解答 解:(1)在AB上截取AG=AD,连接CG.
∵AC平分∠MAB,
∴∠DAC=∠CAB(角平分线定义),
在△ADC和△AGC中,
$\left\{\begin{array}{l}{AC=AC(公共边)}\\{∠DAC=∠CAB(已证)}\\{AD=AG(辅助线的作法)}\end{array}\right.$,
∴△ADC≌△AGC(SAS),
∴∠DCA=∠ACG(全等三角形的对应边相等),
∵AM∥BN(已知),
∴∠DAB+∠ABE=180°(两直线平行,同旁内角互补)
即:∠DAC+∠CAB+∠GBC+∠CBE=180°,
∵∠DAC=∠CAB,∠GBC=∠CBE(角平线定义),
∴∠CAB+∠GBC=90°,
∴∠ACB=90°(三角形内角和定理)
即∠ACG+∠GCB=90°,
∵∠DCA+∠ACG+∠GCB+∠BCE=180°,
∴∠DCA+∠BCE=90°,
∴∠GCB=∠ECB(等角的余角相等),
在△BGE和△BEC中,
$\left\{\begin{array}{l}{∠GCB=∠ECB(已证)}\\{∠ABC=∠CBE(已证)}\\{BC=BC(公共边)}\end{array}\right.$,
∴△BGC≌△BEC(AAS).
∴BG=BE(全等三角形的对应边相等)
∴AD+BE=AG+BG,AD+BE=AB.
(2)当点D在射线AM上、点E在射线BN的反向延长线上时(如图②),AD-BE=AB.
当点D在射线AM的反向延长线上,点E在射线BN上时(如图③),BE-AD=AB.
(3)如图①,设△ABC边上的高为hAB,则
${S}_{△ABC}=\frac{1}{2}AB•{h}_{AB}$,${S}_{△ADC}={S}_{△AGC}=\frac{1}{2}AG•{h}_{AB}$,
∵S△ABC=2S△AD
∴$\frac{1}{2}AB•{h}_{AB}=2×\frac{1}{2}AG•{h}_{AB}$,
∴AB=2AG,BG=AG,
在Rt△ABC中,∠C=90°,∠BAC=30°,
AB=2CB,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{3}$BC,
又∵${S}_{△ABC}=2\sqrt{3}$,
∴$\frac{1}{2}AC•BC=2\sqrt{3}$,$\frac{1}{2}×\sqrt{3}BC•BC=2\sqrt{3}$,
∴BC=2,AB=4,
∴AG=BG=2,
∴BE=BG=2.
点评 本试题是证明线段的和差问题,常常利用“截长补短”的方法,即:在较长线段上截取一段线等于已知线段,把各线段放在一条线段上,利用线段和差求解.此类题常要借助全等三角形来解决.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 26cm | B. | 52cm | C. | 78cm | D. | 104cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
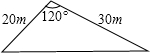 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )
某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价a元,则购买这种草皮至少需要( )| A. | $450\sqrt{3}a$元 | B. | $225\sqrt{3}a$元 | C. | $150\sqrt{3}a$元 | D. | $300\sqrt{3}a$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 水位下降12cm | B. | 水位上升12cm | C. | 水位下降6cm | D. | 水位上升6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com