
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上的动点,连接
上的动点,连接![]() ,将
,将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,设
,设![]()
![]() ,
,

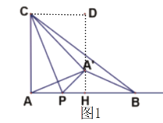
(1)如图1,当点![]() 在
在![]() 上时,求
上时,求![]() 的值.
的值.
(2)如图2,连接![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
(3)在点![]() 的运动过程中,当
的运动过程中,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)由勾股定理求得BC=10,由折叠性质得![]() P=AP=x, C
P=AP=x, C![]() =AC=6,则PB=8-x,
=AC=6,则PB=8-x,![]() B=4,在RtΔ
B=4,在RtΔ![]() BP中,由勾股定理列方程可求得x值;
BP中,由勾股定理列方程可求得x值;
(2)根据已知求出![]() ,由
,由![]() =
=![]() 即可解答;
即可解答;
(3)分情况讨论:①当![]() 时;②当
时;②当![]() 时;③当
时;③当![]() 时,分别求解即可.
时,分别求解即可.
(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴由勾股定理得:BC=10,
由折叠性质得:![]() P=AP=x, C
P=AP=x, C![]() =AC=6,则PB=8-x,
=AC=6,则PB=8-x,![]() B=4,
B=4,
在RtΔ![]() BP中,由勾股定理得:42+x2=(8-x)2,
BP中,由勾股定理得:42+x2=(8-x)2,
解得:![]() ;
;
(2)当![]() 时,
时,
由折叠性质得:AC=![]() C=4,∠CAB=∠C
C=4,∠CAB=∠C![]() P=90,
P=90,
∴![]() =
=![]() ,
,
∵![]() =90,
=90,![]() =90,
=90,
∴![]() ,
,
∵![]() =90,
=90,![]() =90,
=90,
∴![]() ,
,
∴![]() ,
,
∴![]() =4,
=4,
则![]() ,且
,且![]() =
=![]() ,
,
由![]() ,∠CAB=90,可求得
,∠CAB=90,可求得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ;
;
(3)①当![]() 时,若
时,若![]() 在线段
在线段![]() 上,如图1,过
上,如图1,过![]() 作
作![]() H⊥AB于H,过C作CD⊥H
H⊥AB于H,过C作CD⊥H![]() 延长线于D,
延长线于D,
则四边形ACDH是矩形,又![]() 是等腰三角形,
是等腰三角形,
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∵![]() =90,
=90,![]() =90,
=90,
∴![]() ,又
,又![]() =90,
=90,
∴![]() ,
,
∴![]() ,
,
得![]() ,解得
,解得![]() ,
,
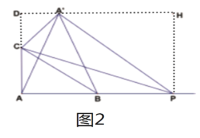
若![]() 在
在![]() 延长线上时,如图2,过
延长线上时,如图2,过![]() 作AB的平行线,交AC延长线与D,过P作PH垂直平行线于H,则四边形APHD是矩形,
作AB的平行线,交AC延长线与D,过P作PH垂直平行线于H,则四边形APHD是矩形,
同上方法,易求得![]() D=4,
D=4,![]() ,
,
∴PH=AD=![]() ,
,
同理可证得![]() ,
,
∴![]() ,
,
得![]() ,解得
,解得![]() ,
,
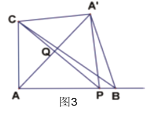
②当![]() 时,如图3,由折叠性质得:
时,如图3,由折叠性质得:
CP垂直平分A![]() ,
,
则![]() ,∠AQP=90,
,∠AQP=90,
又AC=6,
![]() ,
,
∵∠ AQP=∠CAB=90,
∴由同角的余角相等得:∠ACQ=∠QAP,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() ;
;
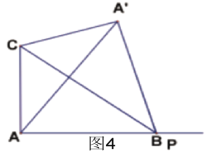
③当![]() 时,如图4,则
时,如图4,则![]() 、
、![]() 重合,
重合,![]() ,
,
综上所述![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
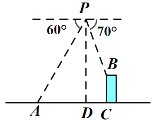
【题目】如图,无人机在600米高空的P点,测得地面A点和建筑物BC的顶端B的俯角分别为60°和70°,已知A点和建筑物BC的底端C的距离为286![]() 米,求建筑物BC的高.(结果保留整数,参考数据:
米,求建筑物BC的高.(结果保留整数,参考数据:![]() ≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难,八方支援.“新冠肺炎”疫情来袭,除了医务人员主动请缨逆行走向战场外,众多企业也伸出援助之手.某公司用甲,乙两种货车向武汉运送爱心物资,两次满载的运输情况如下表:
甲种货车辆数 | 乙种货车辆数 | 合计运物资吨数 | |
第一次 | 3 | 4 | 29 |
第二次 | 2 | 6 | 31 |
(1)求甲、乙两种货车每次满载分别能运输多少吨物资;
(2)目前有46.4吨物资要运输到武汉,该公司拟安排甲乙货车共10辆,全部物资一次运完,其中每辆甲车一次运送花费500元,每辆乙车一次运送花费300元,请问该公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.
(1)求每次降价的百分率.
(2)若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
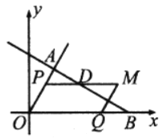
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 、
、![]() 分别是射线
分别是射线![]() 、线段
、线段![]() 上的点,且
上的点,且![]() ,以
,以![]() 、
、![]() 为邻边构造平行四边形
为邻边构造平行四边形![]() ,①若线段
,①若线段![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,则
时,则![]() _______;②把
_______;②把![]() 沿着
沿着![]() 进行折叠,当折叠后
进行折叠,当折叠后![]() 与
与![]() 的重叠部分的面积是平行四边形
的重叠部分的面积是平行四边形![]() 的
的![]() 时,则
时,则![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
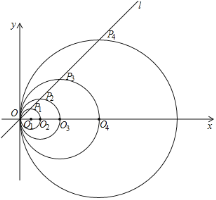
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2;以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3;以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长___________.
的长___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
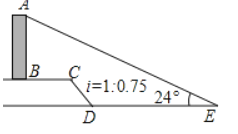
【题目】如图,![]() 是一垂直于水平面的建筑物,某同学从建筑物底端
是一垂直于水平面的建筑物,某同学从建筑物底端![]() 出发,先沿水平方向向右行走
出发,先沿水平方向向右行走![]() 米到达点
米到达点![]() 再经过段坡度(或坡比)为
再经过段坡度(或坡比)为![]() 坡长为
坡长为![]() 米的斜坡
米的斜坡![]() 到达点
到达点![]() 然后再沿水平方向向右行走
然后再沿水平方向向右行走![]() 米到达点
米到达点![]() 均在同一平面内).在
均在同一平面内).在![]() 处测得建筑物顶端
处测得建筑物顶端![]() 的仰角为
的仰角为![]() 求建筑物
求建筑物![]() 的高度. (参考数据:
的高度. (参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张矩形ABCD纸片中,AD=30,AB=25,先将这张纸片沿着过点A的直线折叠,使得点B落在矩形的对称轴上,折痕交矩形的边于点E,则折痕AE的长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com