
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,AC与⊙O交于D,OE∥BD交⊙O于E.
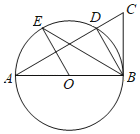
(1)求证:BE平分∠ABD.
(2)当∠A=∠E,BC=2时,求⊙O的面积.
【答案】(1)见解析;(2)⊙O的面积为3π.
【解析】
(1)根据等腰三角形的性质得到∠E=∠ABE,根据平行线的性质得到∠E=∠EBD,等量代换得到∠OBE=∠EBD,于是得到结论;
(2)根据圆周角定理得到∠ADB=90°,得到∠A=30°,根据切线的性质得到∠ABC=90°,解直角三角形即可得到结论.
(1)证明:∵OE=OB,
∴∠E=∠ABE,
∵OE∥BD,
∴∠E=∠EBD,
∴∠OBE=∠EBD,
∴BE平分∠ABD;
(2)解:∵∠A=∠E,
∴∠ABD=2∠A,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A=30°,
∵BC是⊙O的切线,
∴∠ABC=90°,
∵BC=2,
∴AB=![]() BC=2
BC=2![]() ,
,
∴AO=![]() ,
,
∴⊙O的面积=3π.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将正面分别标有数字![]() ,
,![]() ,
,![]() ,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
,背面花色相同的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求这张卡片上的数字为偶数的概率;
(2)随机地抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数恰好为“![]() ”的概率是多少?
”的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D在AB的延长线上,点C、E是⊙O上的两点,CE=CB,![]() ,延长AE交BC的延长线于点F.
,延长AE交BC的延长线于点F.

(1)求证:CD是⊙O的切线;
(2)求证:CE=CF
(3)若BD=1,![]() ,求直径AB的长.
,求直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为实数,关于x的方程为x2+(k+2)x+2k=1.
(1)判断方程有无实数根.
(2)当方程的根和k都是有理数时,请直接写出其中k的1个值和相应方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米. 点
厘米. 点![]() 沿
沿![]() 边从
边从![]() 开始向点
开始向点![]() 以2厘米/秒的速度移动;点
以2厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以1厘米/秒速度移动.如果
以1厘米/秒速度移动.如果![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间
(秒)表示移动的时间![]() ,那么:
,那么:
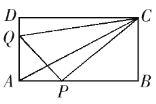
(1)当![]() 为何值时,
为何值时,![]() 为等腰直角三角形?
为等腰直角三角形?
(2)求四边形![]() 的面积;提出一个与计算结果有关的结论;
的面积;提出一个与计算结果有关的结论;
(3)当![]() 为何值时,以点
为何值时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是抛物线![]() 对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.
对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形纸片![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,折叠正方形纸片
,折叠正方形纸片![]() ,使
,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,展开后,折痕
重合,展开后,折痕![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形;⑤
是菱形;⑤![]() ,其中正确结论的序号是______.
,其中正确结论的序号是______.
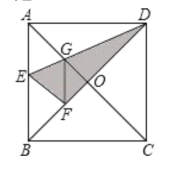
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com