
 如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )
如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )| A. | $50\sqrt{3}+1$ | B. | $50\sqrt{3}$ | C. | 51 | D. | 101 |
分析 设AG=x,分别在Rt△AEG和Rt△ACG中,表示出CG和GE的长度,然后根据DF=100m,求出x的值,继而可求出电视塔的高度AH.
解答 解:设AG=x,
在Rt△AEG中,
∵tan∠AEG=$\frac{AG}{EG}$,
∴EG=$\frac{AG}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$x,
在Rt△ACG中,
∵tan∠ACG=$\frac{AG}{CG}$,
∴CG=$\frac{x}{tan30°}$=$\sqrt{3}$x,
∴$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=100,
解得:x=50$\sqrt{3}$.
则AB=50$\sqrt{3}$+1(米).
故选:A.
点评 本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解,注意利用两个直角三角形的公共边求解是解答此类题型的常用方法.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=-6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=-6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”| A. | 9x+11=6x-16 | B. | 9x-11=6x+16 | C. | $\frac{x-11}{9}=\frac{x+16}{6}$ | D. | $\frac{x+11}{9}=\frac{x-16}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
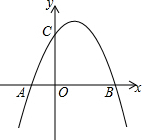 如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.
如图,已知c>0,抛物线y=-x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 列方程解应用题
列方程解应用题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com