
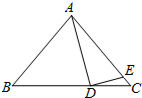
 如图,在△ABC中,AB=AC,点D是BC上一点,点E是AC上一点,且DE⊥AD.若∠BAD=55°,∠B=50°,求∠DEC的度数.
如图,在△ABC中,AB=AC,点D是BC上一点,点E是AC上一点,且DE⊥AD.若∠BAD=55°,∠B=50°,求∠DEC的度数. 科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
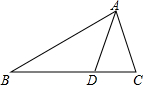 如图,在△ABC中,∠B=30°,∠C=70°,AD是△ABC的一条角平分线,则∠CAD的度数为( )
如图,在△ABC中,∠B=30°,∠C=70°,AD是△ABC的一条角平分线,则∠CAD的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=-6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=-6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”| A. | 9x+11=6x-16 | B. | 9x-11=6x+16 | C. | $\frac{x-11}{9}=\frac{x+16}{6}$ | D. | $\frac{x+11}{9}=\frac{x-16}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com