
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 二次函数
二次函数![]() 的图象经过
的图象经过![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
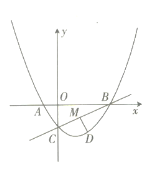
![]() 求二次函数的解析式及点
求二次函数的解析式及点![]() 的坐标.
的坐标.
![]() 点
点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上.设点
下方的二次函数图象上.设点![]() 的横坐标为
的横坐标为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 求线段
求线段![]() 的长关于
的长关于![]() 的函数解析式,并求线段
的函数解析式,并求线段![]() 的最大值.
的最大值.
【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]()
![]() ,
,![]() 有最大值
有最大值![]()
【解析】
(1)根据一次函数的解析式,可得B,C的坐标,由待定系数法,可求得二次函数的解析式;
(2)过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,由D,H的坐标特征,可设
,由D,H的坐标特征,可设![]() ,
,![]() ,易得BOC~DMH,从而得
,易得BOC~DMH,从而得![]() ,进而即可得到结论.
,进而即可得到结论.
(1)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴令y=0,得![]() ,解得:x=4,令x=0,得:y=-2,
,解得:x=4,令x=0,得:y=-2,
∴点![]() 的坐标分别为
的坐标分别为![]() .
.
将点![]() 的坐标代入二次函数的解析式得:
的坐标代入二次函数的解析式得:![]() ,解得:
,解得: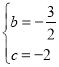 ,
,
∴二次函数的解析式为:![]() ,
,
当![]() 时,
时,![]() ,解得:
,解得:![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
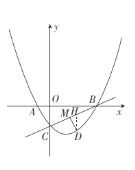
(2)过点![]() 作
作![]() 轴的平行线与
轴的平行线与![]() 交于点
交于点![]() ,
,
∵OB=4,OC=2,
∴BC=![]() ,
,
∵点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上,
下方的二次函数图象上,
∴点![]() ,点
,点![]() (0<m<4),
(0<m<4),
∵DH∥y轴,
∴∠OCB=∠MHD,
∵∠OCB+∠OBC=∠MHD+∠MDH=90°,
∴![]() ,
,
∵∠BOC=∠DMH=90°,
∴BOC~DMH,
∴![]() ,
,
![]()
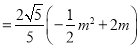
![]() ,(0<m<4),
,(0<m<4),
![]() ,
,
∴当m=2时,![]() 的最大值=
的最大值=![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
【题目】“五一”期间甲乙两商场搞促销活动,甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”“20元”“30元”“50元”,顾客每消费满300元就可从箱子里不放回地摸出2个球,根据两个小球所标金额之和可获相应价格的礼品;乙商场的方案是:在一个不透明的箱子里放2个完全相同的小球,球上分别标“5元”“30元”,顾客每消费满100元,就可从箱子里有放回地摸出1个球,根据小球所标金额可获相应价格的礼品.某顾客准备消费300元.
(1)请用画树状图或列表法,求出该顾客在甲商场获得礼品的总价值不低于50元的概率;
(2)判断该顾客去哪个商场消费使获得礼品的总价值不低于50元机会更大?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师拿出四张卡片,背面完全一样,正面分别画有:矩形、菱形、等边三角形、圆背面朝上洗匀后先让小明抽出一张,记下形状后放回,洗匀后再让小亮抽出一张请你计算出两次都抽到既是中心对称图形又是轴对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
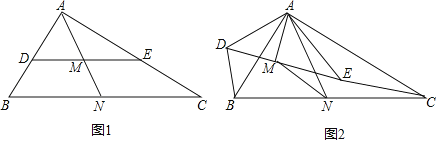
【题目】如图1,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,点D,E,N分别是△ABC的AB,AC,BC边上的中点,连接AN,DE交于点M.
(1)观察猜想:![]() 的值为 :
的值为 :![]() 的值为 ;
的值为 ;
(2)探究与证明:将△ADE绕点A按顺时针方向旋转α角(0°<α<360°),且△ADE内部的线段AM随之旋转,如图2所示,连接BD,CE,MN,试探究线段BD与CE和BD与MN之间分别有什么样的数量关系,并证明;
(3)拓展与延伸:△ADE在旋转的过程中,设直线CE与BD相交于点F,当∠CAE=90°时,BF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
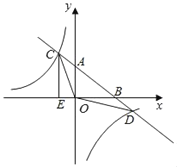
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=![]() ,OB=4,OE=1.
,OB=4,OE=1.
(1)求一次函数的解析式和反比例函数的解析式
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
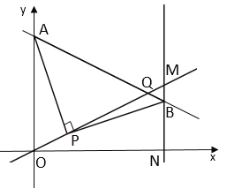
【题目】如图,平面直角坐标系中,已知直线![]() 经过点P(2,1),点A在y轴的正半轴上,连接PA,将线段PA绕点P顺时针旋转90°至线段PB,过点B作直线MN⊥x轴,垂足为N,交直线y=kx(k≠0)于点M(点M在点B的上方),且BN=3BM,连接AB,直线AB与直线
经过点P(2,1),点A在y轴的正半轴上,连接PA,将线段PA绕点P顺时针旋转90°至线段PB,过点B作直线MN⊥x轴,垂足为N,交直线y=kx(k≠0)于点M(点M在点B的上方),且BN=3BM,连接AB,直线AB与直线![]() 交于点Q,则点Q的坐标为__________.
交于点Q,则点Q的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
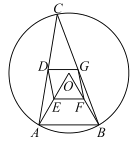
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.
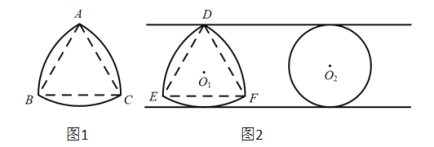
下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com