
【题目】数学老师拿出四张卡片,背面完全一样,正面分别画有:矩形、菱形、等边三角形、圆背面朝上洗匀后先让小明抽出一张,记下形状后放回,洗匀后再让小亮抽出一张请你计算出两次都抽到既是中心对称图形又是轴对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
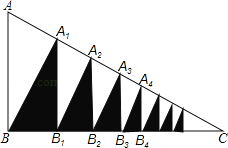
【题目】如图,在Rt△ABC中,AB=3,BC=4,∠ABC=90°,过B作A1B⊥AC,过A1作A1B1⊥BC,得阴影Rt△A1B1B;再过B1作B1A2⊥AC,过A2作A2B2⊥BC,得阴影Rt△A2B2B1;…如此下去.请猜测这样得到的所有阴影三角形的面积之和为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() 是
是![]() 上一点,点
上一点,点![]() 从点
从点![]() 沿折线
沿折线![]() 运动到点
运动到点![]() 时停止;点
时停止;点![]() 从点
从点![]() 沿
沿![]() 运动到点
运动到点![]() 时停止,速度均为每秒1个单位长度.如果点
时停止,速度均为每秒1个单位长度.如果点![]() ,
,![]() 同时开始运动,设运动时间为
同时开始运动,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,已知
,已知![]() 与
与![]() 的函数图象如图2所示,有以下结论:
的函数图象如图2所示,有以下结论:
①![]() ;
;
②![]() ;
;
③当![]() 时,
时,![]() ;
;
④当![]() 时,
时,![]() 是等腰三角形;
是等腰三角形;
⑤当![]() 时,
时,![]() .
.
其中正确的有( ).

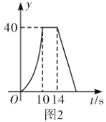
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴于点
轴于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,与抛物线另一个交点为
,与抛物线另一个交点为![]() ,点
,点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方,且
上方,且![]() 是以
是以![]() 为腰的等腰三角形时,求点
为腰的等腰三角形时,求点![]() 的坐标;
的坐标;
(3)如图2,连接![]() ,以点
,以点![]() 为直角顶点,线段
为直角顶点,线段![]() 为较长直角边,构造两直角边比为1:2的
为较长直角边,构造两直角边比为1:2的![]() ,是否存在点
,是否存在点![]() ,使点
,使点![]() 恰好落在直线
恰好落在直线![]() 上?若存在,请直接写出相应点
上?若存在,请直接写出相应点![]() 的横坐标(写出两个即可);若不存在,请说明理由.
的横坐标(写出两个即可);若不存在,请说明理由.
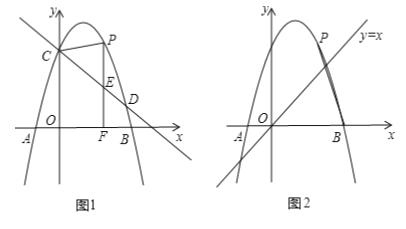
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
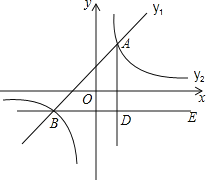
查看答案和解析>>
科目:初中数学 来源: 题型:
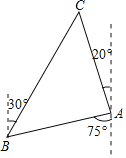
【题目】如图,一艘渔船位于灯塔A的南偏西75°方向的B处,距离A处30海里,渔船沿北偏东30°方向追寻鱼群,航行一段时间后,到达位于A处北偏西20°方向的C处,渔船出现了故障立即向正在灯塔A处的巡逻船发出求救信号.巡逻船收到信号后以40海里每小时的速度前往救助,请问巡逻船多少分钟能够到达C处?(参考数据:![]() ≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
查看答案和解析>>
科目:初中数学 来源: 题型:
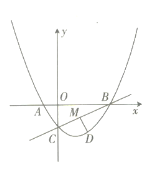
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 二次函数
二次函数![]() 的图象经过
的图象经过![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
![]() 求二次函数的解析式及点
求二次函数的解析式及点![]() 的坐标.
的坐标.
![]() 点
点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上.设点
下方的二次函数图象上.设点![]() 的横坐标为
的横坐标为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 求线段
求线段![]() 的长关于
的长关于![]() 的函数解析式,并求线段
的函数解析式,并求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
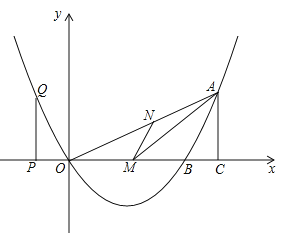
【题目】如图,已知二次函数的图象过点![]() .
.![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的长;
的长;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴与抛物线交于
轴与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,当以
,当以![]() 为顶点的三角形与以
为顶点的三角形与以![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com