
【题目】某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝.其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线![]() 、
、![]() 与半圆相切,上、下桥斜面的坡度
与半圆相切,上、下桥斜面的坡度![]() ,桥下水深
,桥下水深![]() 米.水面宽度
米.水面宽度![]() 米.设半圆的圆心为
米.设半圆的圆心为![]() ,直径
,直径![]() 在坡角顶点
在坡角顶点![]() 、
、![]() 的连线上.求从
的连线上.求从![]() 点上坡、过桥、下坡到
点上坡、过桥、下坡到![]() 点的最短路径长.(参考数据:
点的最短路径长.(参考数据:![]() ,
,![]() ,
,![]() )
)

【答案】从![]() 点上坡、过桥、下坡到
点上坡、过桥、下坡到![]() 点的最短路径长为
点的最短路径长为![]() 米.
米.
【解析】
首先明确从M点上坡、过桥、下坡到N点的最短路径长应为如图ME+![]() +FN,连接如图,把实际问题转化为直角三角形问题,由已知求出OD即半径,再由坡度i=1:3.7和tan15°=
+FN,连接如图,把实际问题转化为直角三角形问题,由已知求出OD即半径,再由坡度i=1:3.7和tan15°=![]() =1:3.7,得出∠M=∠N=15°,因此能求出ME和FN,所以求出∠EOM=∠FON=90°-15°=75°,则得出
=1:3.7,得出∠M=∠N=15°,因此能求出ME和FN,所以求出∠EOM=∠FON=90°-15°=75°,则得出![]() 所对的圆心角∠EOF,相继求出
所对的圆心角∠EOF,相继求出![]() 的长,从而求出从M点上坡、过桥、下坡到N点的最短路径长.
的长,从而求出从M点上坡、过桥、下坡到N点的最短路径长.
连接FO、EO、DO,
已知CD=24m,0P=5m,∴PD=12m,
∴OD2=OP2+PD2=52+122=169,
∴OD=13m,则OE=OF=13m,
已知坡度i=1:3.7和tan15°=![]() =1:3.7,
=1:3.7,
∴∠M=∠N=15°,
∴cot15°=![]() =2+
=2+![]() ,
,
∵上、下桥的坡面线ME、NF与半圆相切,
∴tan∠M=OE:EM,
∴ME=FN=![]() =13×(2+
=13×(2+![]() ),=26+13
),=26+13![]() (m),
(m),
∠EOM=∠FON=90°-15°=75°,
∴∠EOF=180°-75°-75°=30°,
∴![]() =
=![]() =
=![]() π(m)
π(m)
∴ME+![]() +FN=26+13
+FN=26+13![]() +
+![]() π+26+13
π+26+13![]() ≈102.7(m)
≈102.7(m)
答:从![]() 点上坡、过桥、下坡到
点上坡、过桥、下坡到![]() 点的最短路径长为
点的最短路径长为![]() 米.
米.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在![]() 处用高
处用高![]() 米(
米(![]() 米)的测角仪测得旗杆
米)的测角仪测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,再向旗杆方向前进
,再向旗杆方向前进![]() 米到
米到![]() 处,又测得旗杆顶端
处,又测得旗杆顶端![]() 的仰角为
的仰角为![]() ,请求出旗杆
,请求出旗杆![]() 的高度(取
的高度(取![]() ,结果保留整数)
,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
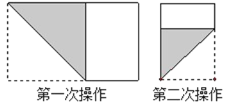
【题目】如图,动手操作:长为1,宽为a的长方形纸片(![]() <a<l),如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的长方形为正方形,则操作终止.当n=3时,a的值为( )
<a<l),如图那样折一下,剪下一个边长等于长方形宽度的正方形(称为第一次操作);再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的长方形为正方形,则操作终止.当n=3时,a的值为( )
A.![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
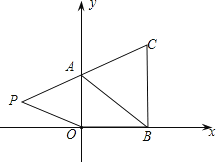
【题目】如图,在下面直角坐标系中,已知![]() ,
,![]() ,
,![]() 三点,其中
三点,其中![]() 、
、![]() 、
、![]() 满足关系式
满足关系式![]() ,
,![]() .
.
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)如果在第二象限内有一点![]() ,请用含
,请用含![]() 的式子表示四边形
的式子表示四边形![]() 的面积;
的面积;
(3)在(2)的条件下,是否存在点![]() ,使四边形
,使四边形![]() 的面积与
的面积与![]() 的面积相等?若存在,求出点
的面积相等?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
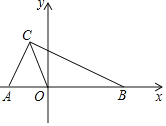
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|a+2|+(b﹣4)2=0
(1)求a,b的值;
(2)在y轴上是否存在一点M,使△COM的面积=![]() △ABC的面积,求出点M的坐标.
△ABC的面积,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC,CD于E、F.
(1)试说明△CEF是等腰三角形.
(2)若点E恰好在线段AB的垂直平分线上,试说明线段AC与线段AB之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com