
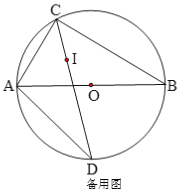
【题目】如图,⊙![]() 是Rt△ABC的外接圆,∠ACB=90°,点I是△ABC的内心,CI的延长线交⊙O于点D,连接AD.
是Rt△ABC的外接圆,∠ACB=90°,点I是△ABC的内心,CI的延长线交⊙O于点D,连接AD.
(1)求证:DA=DI.
(2)若AB=10,AC=6,求AD、CD的长.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
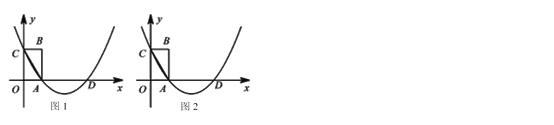
【题目】如图,在平面直角坐标系中,矩形OABC的边OA,OC分别位于x轴,y轴上,经过A,C两点的抛物线变x轴于另一点D,连接AC.请你只用无刻度的直尺按要求画图.
(1)在图1中的抛物线上,画出点E,使DE=AC;
(2)在图2中的抛物线上,画出抛物线的顶点F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(a﹣1)x2+3x﹣6的图象与x轴的交点为A和B,若点B一定在坐标原点和(1,0)之间,且B点不与原点和(1,0)重合,那么a的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在人教版八年级上册数学教材P53的数学活动中有这样一段描述:在四边形ABCD中,若AD=CD,AB=CB,则我们把这种两组邻边分别相等的四边形叫做“筝形”,试猜想筝形的角.对角线有什么性质?然后选择其中一条性质用全等三角形的知识证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB至点F,使BF=BD连接AF.
(1)求证:AF=CD.
(2)若CE平分∠ACB交AB于点E,试猜想AC,AF,AE三条线段之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
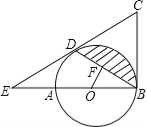
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
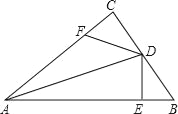
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
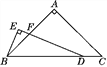
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )
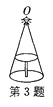
A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com