
如图AB∥CD,∠NCM=90°,∠NCB=30°,CM平分∠BCE,求∠B的大小.

60°
【解析】
试题分析:由CM平分∠BCE可得∠BCE=2∠BCM,由∠NCM=90°,∠NCB=30°可得∠BCM的度数,从而得到∠BCE的度数,再根据平行线的性质即得结果。
因为CM平分∠BCE,
所以∠BCE=2∠BCM.
因为∠NCM=90°,∠NCB=30°,
所以∠BCM=60°.
所以∠BCE=120°.
根据两直线平行,同旁内角互补,
因为AB∥CD,
所以∠BCE+∠B=180°.
所以∠B=60°.
考点:本题考查的是角平分线的性质,平行线的性质
点评:解答本题的关键是熟练掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2011-2012学年福建仙游郊尾沙溪中学七年级下学期第二次月考数学卷(带解析) 题型:解答题
如图,E、F分别是AB、CD上一点,∠2=∠D,∠1与∠C互余,EC⊥AF,试说明AB∥CD(10分) 
填空: 因为 ∠2=∠D
所以 AF∥
因为 EC⊥AF
所以 ED⊥
所以 ∠C与∠D
又因为 ∠1与∠C互余
所以 ∠1=
所以 AB∥
查看答案和解析>>
科目:初中数学 来源:2012年苏教版初中数学七年级下 7.1探索直线平行的条件练习卷(解析版) 题型:解答题
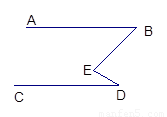
已知:如图,AB、BE、ED、CD依次相交于B、E、D,∠E=∠B+∠D.
试说明AB∥CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com