
【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC的度数为( )

A.35°B.40°C.45°D.60°
【答案】C
【解析】
根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,然后求出△ABE是等腰直角三角形,根据等腰直角三角形的性质求出∠BAE=∠ABE=45°,再根据等腰三角形两底角相等求出∠ABC,然后求出∠CBE,根据等腰三角形三线合一的性质可得BF=CF,根据直角三角形斜边上的中线等于斜边的一半可得BF=EF,根据等边对等角求出∠BEF=∠CBE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
∵DE垂直平分AB,
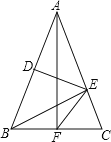
∴AE=BE,
∵BE⊥AC,
∴△ABE是等腰直角三角形,
∴∠BAE=∠ABE=45°,
又∵AB=AC,
∴∠ABC=![]() (180°-∠BAC)=
(180°-∠BAC)=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠CBE=∠ABC-∠ABE=67.5°-45°=22.5°,
∵AB=AC,AF⊥BC,
∴BF=CF,
∵EF=![]() BC(直角三角形斜边中线等于斜边的一半),
BC(直角三角形斜边中线等于斜边的一半),
∴BF=EF=CF,
∴∠BEF=∠CBE=22.5°,
∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点的坐标分别为(﹣2,2)、(1,8).

(1)求三角形ABO的面积;
(2)若y轴上有一点M,且三角形MAB的面积为10,求M点的坐标;
(3)如图,把直线AB以每秒2个单位的速度向右平移,问经过多少秒后,该直线与y轴交于点(0,﹣2)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )

A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AF分别与BD、CE交于点G、H,∠1=54°,∠2=126°.
(1)求证:BD∥CE;
(2)若AC⊥CE于C,交BD于B,FD⊥BD于D,交CE于E,探索∠A与∠F的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:
1×2×3×4+1=________;
2×3×4×5+1=_______;
3×4×5×6+1=_______;
4×5×6×7+1=________;
(2)观察上述计算的结果,指出他们的共同特性;
(3)以上特性,对于任意给出的四个连续自然数的积与1的和仍具备吗?试证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有四个小球,球上分别标有![]() ,
,![]() ,0,1四个数字,这些小球除数字外都相同.
,0,1四个数字,这些小球除数字外都相同.
![]() 如果从袋中任意摸出一个小球,那么小球上的数字标有“
如果从袋中任意摸出一个小球,那么小球上的数字标有“![]() “的概率是______
“的概率是______
![]() 甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为
甲、乙两人玩“猜数字”游戏,甲先从袋中任意摸出一个小球,将小球上的数字记为m,再由乙猜这个小球上的数字,记为![]() 如果m,n满足
如果m,n满足![]() ,那么就称甲、乙两人“心有灵犀”
,那么就称甲、乙两人“心有灵犀”![]() 请用列表法
请用列表法![]() 或画树状图法
或画树状图法![]() 求两人“心有灵犀”的概率.
求两人“心有灵犀”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某工艺厂设计了一款成本为10元![]() 件的工艺品投放市场进行试销,经过调查,得到如下数据:
件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 |
| 20 | 30 | 40 | 50 |
|
每天销售量 |
| 500 | 400 | 300 | 200 |
|
![]() 猜一猜y是x的什么函数关系?并求出此函数的关系式;
猜一猜y是x的什么函数关系?并求出此函数的关系式;
![]() 若用
若用![]() 元
元![]() 表示工艺厂试销该工艺品每天获得的利润,试求
表示工艺厂试销该工艺品每天获得的利润,试求![]() 元
元![]() 与/span>
与/span>![]() 元
元![]() 件
件![]() 之间的函数关系式.
之间的函数关系式.
![]() 若该工艺品的每天的总成本不能超过2500元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
若该工艺品的每天的总成本不能超过2500元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
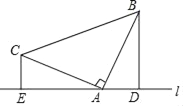
【题目】已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线l的垂线段BD、CE,垂足分别D、E.
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请画出图形,直接给出你的结论(不用证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A(t,1)是平面直角坐标系中第一象限的点,点B,C分别是y轴负半轴和x轴正半轴上的点,连接AB,AC,BC.
(1)如图1,若OB=1,OC =![]() ,且A,B,C在同一条直线上,求t的值;
,且A,B,C在同一条直线上,求t的值;

(2)如图 2,当 t =1,∠ACO +∠ACB = 180°时,求 BC + OC -OB 的值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com