Question

【题目】已知事件“在矩形ABCD的边CD上随机取一点P，使△APB的最大边是AB”发生的概率为 ，则 =（ ）
A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：记“在矩形ABCD的边CD上随机取一点P，使△APB的最大边是AB”为事件M，试验的全部结果构成的长度即为线段CD， 若△APB的最大边是AB”发生的概率为 ，
则 = ，
设AD=y，AB=x，则DE= x，PE= DE= x，
则PC= x+ x= x，
则PB2=AB2时，
PC2+BC2=PB2=AB2 ，
即（ x）2+y2=x2 ，
即 x2+y2=x2 ，
则y2= x2 ，
则y= x，
即 = ，
即 = ，
故选：C．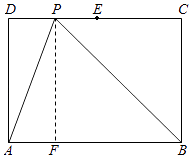

先明确是一个几何概型中的长度类型，然后求得事件“在矩形ABCD的边CD上随机取一点P，使△APB的最大边是AB”发生的线段长度，再利用两者的比值即为发生的概率 ，从而求出 ．