
【题目】如图1,地面BD上两根等长立柱AB,CD之间有一根绳子可看成抛物线y=0.1x2﹣0.8x+5.
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为5米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面2米,求MN的长;
(3)将立柱MN的长度提升为5米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() .设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
.设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,但2≤k≤3时,求m的取值范围.
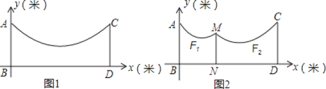
【答案】(1)![]() 米;(2)
米;(2)![]() 米;(3)2≤m≤8﹣2
米;(3)2≤m≤8﹣2![]() .
.
【解析】
(1)直接利用配方法求出二次函数最值得出答案;
(2)利用顶点式求出抛物线F1的解析式,进而得出x=5时,y的值,进而得出MN的长;
(3)根据题意得出抛物线F2的解析式,得出k的值,进而得出m的取值范围.
解:(1)∵a=0.1>0,
∴抛物线顶点为最低点,
∵y=0.1x2﹣0.8x+5=0.1(x﹣4)2+![]() ,
,
∴绳子最低点离地面的距离为:![]() 米;
米;
(2)由(1)可知,对称轴为x=4,则BD=8,
令x=0得y=5,
∴A(0,5),C(8,5),
由题意可得:抛物线F1的顶点坐标为:(4,2),
设F1的解析式为:y=a(x﹣4)2+2,
将(0,5)代入得:16a+2=5,
解得:a=![]() ,
,
∴抛物线F1为:y=![]() (x﹣4)2+2,
(x﹣4)2+2,
当x=5时,y=![]() +2=
+2=![]() ,
,
∴MN的长度为:![]() 米;
米;
(3)∵MN=DC=5,
∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,
∴F2的横坐标为:![]() (8﹣m)+m=
(8﹣m)+m=![]() m+4,
m+4,
∴抛物线F2的顶点坐标为:(![]() m+4,k),
m+4,k),
∴抛物线F2的解析式为:y=![]() (x﹣
(x﹣![]() m﹣4)2+k,
m﹣4)2+k,
把C(8,5)代入得:![]() (8﹣
(8﹣![]() m﹣4)2+k=5,
m﹣4)2+k=5,
解得:k=﹣![]() (4﹣
(4﹣![]() m)2+5,
m)2+5,
∴k=﹣![]() (m﹣8)2+5,
(m﹣8)2+5,
∴k是关于m的二次函数,
又∵由已知m<8,在对称轴的左侧,
∴k随m的增大而增大,
∴当k=2时,﹣![]() (m﹣8)2+5=2,
(m﹣8)2+5=2,
解得:m1=2,m2=14(不符合题意,舍去),
当k=3时,﹣![]() (m﹣8)2+5=3,
(m﹣8)2+5=3,
解得:m1=8﹣2![]() ,m2=8+2
,m2=8+2![]() (不符合题意,舍去),
(不符合题意,舍去),
∴m的取值范围是:2≤m≤8﹣2![]() .
.


科目:初中数学 来源: 题型:
【题目】2019年重庆国际马拉松赛于3月31日在南滨公园鸣枪开跑已知A、B两补给站之间的路程为1470米,志愿者甲、乙都从A站出发支援B站.甲先出发,且在途中停留了4分钟,甲出发6分钟后,乙才从A站出发.在整个行走过程中,两人保持各自速度匀速行走,两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达B站时,甲与B站相距的路程是_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
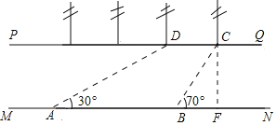
【题目】如图,河流两岸PQ,MN互相平行,C、D是河岸PQ上间隔50m的两个电线杆,某人在河岸MN上的A处测得∠DAB=30°,然后沿河岸走了100m到达B处,测得∠CBF=70°,求河流的宽度(结果精确到个位,![]() =1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
=1.73,sin70°=0.94,cos70°=0.34,tan70°=2.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示折叠,使点D与点O重合,折痕为FG,点F、G分别在AD,BC上,连接OG、DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是
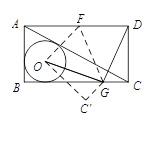
A.CD+DF=4B.CDDF=2![]() 3
3
C.BC+AB=2![]() +4D.BCAB=2
+4D.BCAB=2
查看答案和解析>>
科目:初中数学 来源: 题型:
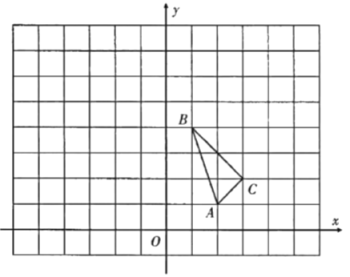
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
请解答下列问题:
(1)画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(2)以原点![]() 为位似中心,位似比为1:2,在
为位似中心,位似比为1:2,在![]() 轴的右侧,画出
轴的右侧,画出![]() 放大后的图形
放大后的图形![]() ,并直接写出
,并直接写出![]() 点的坐标;
点的坐标;
(3)如果点![]() 在线段
在线段![]() 上,请直接写出经过(2)的变化后对应点
上,请直接写出经过(2)的变化后对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
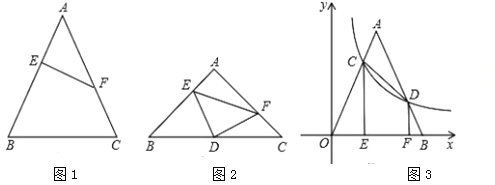
【题目】如图1,等腰![]() 中,点
中,点![]() 分别在腰
分别在腰![]() 上,连结
上,连结![]() ,若
,若![]() ,则称
,则称![]() 为该等腰三角形的逆等线.
为该等腰三角形的逆等线.
(1)如图1,![]() 是等腰
是等腰![]() 的逆等线,若
的逆等线,若![]() ,求逆等线
,求逆等线![]() 的长;
的长;
(2)如图2,若直角![]() 的直角顶点
的直角顶点![]() 恰好为等腰直角
恰好为等腰直角![]() 底边
底边![]() 上的中点,且点
上的中点,且点![]() 分别在
分别在![]() 上,求证:
上,求证:![]() 为等腰
为等腰![]() 的逆等线;
的逆等线;
(3)如图3,等腰![]() 的顶点
的顶点![]() 与原点重合,底边
与原点重合,底边![]() 在
在![]() 轴上,反比例函数
轴上,反比例函数![]() 的图象交
的图象交![]() 于点
于点![]() ,若
,若![]() 恰为
恰为![]() 的逆等线,过点
的逆等线,过点![]() 分别作
分别作![]() 轴于点
轴于点![]() 轴于点
轴于点![]() ,已知
,已知![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com