
分析 (1)根据待定系数法解答即可;
(2)用待定系数法确定函数的解析式,再根据勾股定理解答即可.
解答 解:(1)∵一次函数y=kx+4m(m>0)的图象经过点B(p,2m),
∴2m=kp+4m.
∴kp=-2m.
∵m=1,k=-1,
∴p=2.
∴B(2,2).
(2)线段AB上存在一点N,使得点N到坐标原点O与到点C的距离之和等于线段OB的长.
理由如下:
由题意,将B(p,2m),C(n,0)分别代入y=kx+4m,
得kp+4m=2m且kn+4m=0.
可得n=2p.
∵n+2p=4m,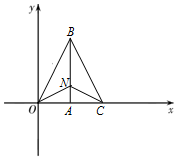
∴p=m.
∴A(m,0),B(m,2m),C(2m,0).
∵xB=xA,
∴AB⊥x轴,
且 OA=AC=m.
∴对于线段AB上的点N,有NO=NC.
∴点N到坐标原点O与到点C的距离之和为NO+NC=2NO.
∵∠BAO=90°,
在Rt△BAO,Rt△NAO中分别有
OB2=AB2+OA2=5m2,NO2=NA2+OA2=NA2+m2.
若2NO=OB,
则4NO2=OB2.
即4(NA2+m2)=5m2.
可得NA=$\frac{1}{2}$m.
即NA=$\frac{1}{4}$AB.
所以线段AB上存在一点N,使得点N到坐标原点O与到点C的距离之和等于线段OB的长,且NA=$\frac{1}{4}$AB.
点评 此题考查点的坐标与解析式的关系以及待定系数法的应用,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
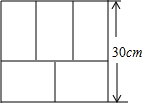 用一元一次方程的知识解决下面的问题:
用一元一次方程的知识解决下面的问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com