
分析 (1)二次函数y=-x2+x+c的图象与x轴只有一个交点,可知△=0,解方程即可解决问题.
(2)根据二次函数的增减性即可解决问题.
解答 解:(1)由题意得△=1+4c=0,
∴c=-$\frac{1}{4}$,
∴y=-x2+x-$\frac{1}{4}$,
∵当x=-$\frac{b}{2a}$=$\frac{1}{2}$时,y=0,∴顶点坐标为($\frac{1}{2}$,0).
(2)∵a=-1<0,开口向下,
∴当x>$\frac{1}{2}$时,y随x的增大而减小.
点评 本题考查二次函数与x轴的交点、待定系数法、二次函数的性质等知识,解题的关键是记住△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
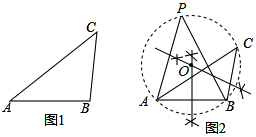 阅读下面材料:
阅读下面材料:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4822×108 | B. | 4.822×1011 | C. | 48.22×1010 | D. | 0.4822×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.
如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=$\frac{10}{3}$或10s时,△POQ是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
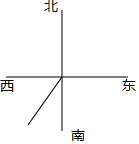 如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )| A. | 南偏东40°方向 | B. | 北偏西50°方向 | C. | 南偏东50°方向 | D. | 东南方向 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com