
【题目】学校组织![]() 名同学和
名同学和![]() 名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为
名教师参加校外学习交流活动现打算选租大、小两种客车,大客车载客量为![]() 人/辆,小客车载客量为
人/辆,小客车载客量为![]() 人/辆
人/辆
(1)学校准备租用![]() 辆客车,有几种租车方案?
辆客车,有几种租车方案?
(2)在(1)的条件下,若大客车租金为![]() 元/辆,小客车租金为
元/辆,小客车租金为![]() 元/辆,哪种租车方案最省钱?
元/辆,哪种租车方案最省钱?
(3)学校临时增加![]() 名学生和
名学生和![]() 名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有
名教师参加活动,每辆大客车有2名教师带队,每辆小客车至少有![]() 名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有
名教师带队.同学先坐满大客车,再依次坐满小客车,最后一辆小客车至少要有![]() 人,请你帮助设计租车方案
人,请你帮助设计租车方案
【答案】(1)有3种租车方案;(2)租5辆大客车,2辆小客车最省钱;(3)租用大客车2辆,小客车7辆;或租10辆小客车.
【解析】
(1)设租大客车x辆,根据题意可列出关于x的不等式,求得不等式的解集后,再根据x为整数即可确定租车方案;
(2)依次计算(1)题中的租车方案,比较结果即可得出答案;
(3)设租大客车x辆,小客车y辆,根据客车的座位数满足的条件可确定x、y满足的不等式组,进一步可确定x、y满足的方程,再由带队的老师数可确定x、y满足的不等式,二者结合即可确定租车方案.
解:(1)由题意知:本次乘车共270+7=277(人).
设租大客车x辆,则小客车(7-x)辆,根据题意,得![]() ,
,
解得:![]() ,
,
因为x为整数,且x≤7,所以x=5,6,7,即有3种租车方案.
(2)方案一:当x=7,所租7辆皆为大客车时,租车费用为:7×400=2800(元),
方案二:当x=6,所租6辆为大客车,1辆为小客车时,租车费用为:6×400+300=2700(元),
方案三:当x=5,所租5辆为大客车,2辆为小客车时,租车费用为:5×400+300×2=2600(元),
所以,租5辆大客车,2辆小客车最省钱.
(3)乘车总人数为270+7+10+4=291(人),因为最后一辆小客车最少20人,则客车空位不能大于10个,所以客车的总座位数应满足:291≤座位数≤301.
设租大客车x辆,小客车y辆,则291≤45x+30y≤301,即![]() ,
,
∵x、y均为整数,∴3x+2y=20,即![]() .
.
∵每辆大客车有2名教师带队,每辆小客车至少有![]() 名教师带队,
名教师带队,
∴2x+y≤11.
把![]() 代入上式,得
代入上式,得![]() ,解得
,解得![]() .
.
又∵x为整数且是2的倍数,∴x=2,y=7或x=0,y=10.
故租车方案为:租大客车2辆,小客车7辆;或租10辆小客车.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
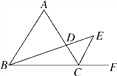
【题目】如图,△ABC是等边三角形,CE是∠ACB的外角平分线,点D在AC上,连接BD并延长交CE于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,横坐标为a的点 A在反比例函数
中,横坐标为a的点 A在反比例函数![]() 的图象上,点
的图象上,点![]() 与点
与点![]() 关于点
关于点![]() 对称,一次函数
对称,一次函数![]() 的图象经过点
的图象经过点![]()
(1)设![]() ,点
,点![]() (4,2)在函数
(4,2)在函数![]() ,
,![]() 的图像上.
的图像上.
①分别求函数![]() ,
,![]() 的表达式;
的表达式;
②直接写出使![]() 成立的
成立的![]() 的范围;
的范围;
(2)如图①,设函数![]() ,
,![]() 的图像相交于点
的图像相交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,△
,△![]() 的面积为16,求
的面积为16,求![]() 的值;
的值;
(3)设![]() ,如图②,过点
,如图②,过点![]() 作
作![]() 轴,与函数
轴,与函数![]() 的图像相交于点
的图像相交于点![]() ,以
,以![]() 为一边向右侧作正方形
为一边向右侧作正方形![]() ,试说明函数
,试说明函数![]() 的图像与线段
的图像与线段![]() 的交点
的交点![]() 一定在函数
一定在函数![]() 的图像上.
的图像上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西南大学银翔实验中学第二届缤纷科技节于2019年5月份隆重举行,主题:绿色体验成长﹣玩出你的稀缺竞争力,本届缤纷科技节有展示类、体验类、竞赛类共40多个项目.4月份,学校对活动中所需物品统一购,其中某一体验类项目需要A、B两种材料,已知A种材料单价32元/套,B种材料单价24元/套,活动需要A、B两种材料共50套计划购买A、B两种材料总费用不超过1392元.
(1)若按计划采购,最多能购买A种材料多少套?
(2)在实际来购过程中,受多方面因素的影响,与(1)中最多购买A种材料的计划相比,实际采购A种材料数量的增加了![]() a%,B种材料的数量减少
a%,B种材料的数量减少![]() a%(A、B材料的数量均为整数),实际采购A种材料的单价减少了
a%(A、B材料的数量均为整数),实际采购A种材料的单价减少了![]() a%,B种材料的单价增加
a%,B种材料的单价增加![]() a%,且实际总费用比按(1)中最多购买A种材料的总费用多了16元,求a.
a%,且实际总费用比按(1)中最多购买A种材料的总费用多了16元,求a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经营甲、乙两种商品,其进价和售价如下表:
甲 | 乙 | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
已知该商店购进了甲、乙两种商品共160件.
(1)若商店在销售完这批商品后要获利1000元,则应分别购进甲、乙两种商品各多少件?
(2)若商店的投入资金少于4300元,且要在售完这批商品后获利不少于1250元,则共有几种购货的方案?其中,哪种购货方案获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
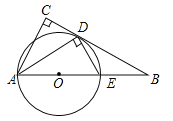
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:

(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com