
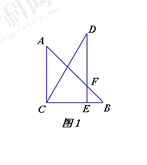
【题目】把一副三角板按如图1所示放置,其中点![]() 在
在![]() 边上,
边上,![]() ,斜边
,斜边![]() .将三角板
.将三角板![]() 绕点
绕点![]() 顺时针旋转,记旋转角为
顺时针旋转,记旋转角为![]() .
.
(1)在图1中,设![]() 与
与![]() 的交点为
的交点为![]() ,则线段AF的长为 ;
,则线段AF的长为 ;
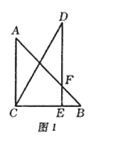
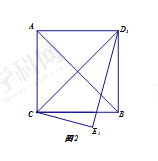
(2)当![]() 时,三角板
时,三角板![]() 旋转到
旋转到![]() ,的位置(如图2所示),连接
,的位置(如图2所示),连接![]() ,请判断四边形
,请判断四边形![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
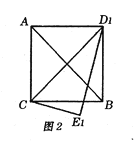
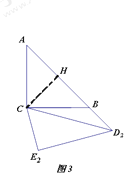
(3)当三角板![]() 旋转到
旋转到![]() 的位置(如图3所示)时,此时点
的位置(如图3所示)时,此时点![]() 恰好在
恰好在![]() 的延长线上.①求旋转角
的延长线上.①求旋转角![]() 的度数;②求线段
的度数;②求线段![]() 的长.
的长.
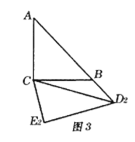
【答案】(1)![]() ;(2)菱形
;(2)菱形![]() 是正方形,见解析;(3)①75°,②
是正方形,见解析;(3)①75°,②![]()
【解析】
(1)根据题意可求得BC,CE的值,从而求得BE的值,再根据![]() 为等腰直角三角形可求得BF的值,最后根据线段的和与差求出AF.
为等腰直角三角形可求得BF的值,最后根据线段的和与差求出AF.
(2)由题意可得出![]() ,在根据旋转的性质即可推出
,在根据旋转的性质即可推出![]() ,得出
,得出![]() 及
及![]() ,推出四边形
,推出四边形![]() 是菱形,最后根据
是菱形,最后根据![]() ,可以推出为正方形.
,可以推出为正方形.
(3)①取![]() 边的中点
边的中点![]() ,连接
,连接![]() ,根据题意得出
,根据题意得出![]() ,
,![]() ,再证明
,再证明![]() ,得出
,得出![]() ,结合题意即可得出旋转角;
,结合题意即可得出旋转角;
![]() 结合题意根据线段的和与差即可得出.
结合题意根据线段的和与差即可得出.
解:(1)![]()
![]() ,斜边
,斜边![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,
![]()
![]() =
=![]()
![]()
![]() .
.
故答案为:![]() ;
;
(2) 四边形![]() 是正方形.
是正方形.
![]()
![]() ,
,
又![]() ,
,
![]() ,
,
同理可证:![]() ,
,
又![]() 四边形
四边形![]() 是菱形,
是菱形,
又![]() 菱形
菱形![]() 是正方形.
是正方形.
(3)①取![]() 边的中点
边的中点![]() ,连接
,连接![]() ,
,
![]() 是等腰直角三角形,且斜边
是等腰直角三角形,且斜边![]() ,且
,且![]() ,
,
![]() 是直角三角形,且斜边
是直角三角形,且斜边![]() ,
,
![]() ,
,
又![]()
![]() ,
,
![]()
又![]() ,
,![]()
又![]() ,
,
则旋转角![]() ;
;
![]()
![]() ,
,![]() ,
,
![]()


科目:初中数学 来源: 题型:
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
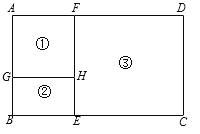
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=10,高AD=8,M、N、P分别在边AB、BC、AC上移动,但不与A、B、C重合,连接MN、NP、MP,且MP始终与BC保持平行,AD与MP相交于点E,设MP=x,△MNP的面积用y表示.
(1)求y关于x的函数关系式;
(2)当x取什么值时,y有最大值,并求出的最大值;
(3)当x取什么值时,△MNP是等腰直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
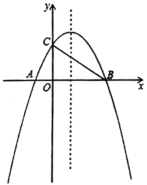
(1)求该抛物线的函数表达式;
(2)若点![]() 为抛物线对称轴上一点,抛物线上是否存在点
为抛物线对称轴上一点,抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点
为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)点![]() 是直线
是直线![]() 上方抛物线上的点,若
上方抛物线上的点,若![]() ,求出
,求出![]() 点的到
点的到![]() 轴的距离.
轴的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地盛产樱桃,一年一度的樱桃节期间,很多果园推出了免费品尝和优惠采摘活动,其中甲、乙两家果园的樱桃品质相同,销售价格也相同,但推出了不同的采摘方案:
甲园 | 游客进园需购买 |
乙园 | 游客进园不需购买门票,采摘的樱桃在一定数量以内按原价购买,超过部分打折购买 |
小明和爸爸、妈妈在樱桃节期间也来采摘樱桃,若设他们的樱桃采摘量为![]() (千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为
(千克)(出园时将自己采摘的樱桃全部购买),在甲采摘园所需总费用为![]() (元)在乙采摘园所需总费用为
(元)在乙采摘园所需总费用为![]() (元),图中的折线
(元),图中的折线![]() 表示
表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)①甲、乙两果园的樱桃单价为_____________元![]() 千克;
千克;
②直接写出![]() 的函数表达式:_________________,并在图中补画出
的函数表达式:_________________,并在图中补画出![]() 的函数图象;
的函数图象;
(2)求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若小明一家当天所采摘的樱桃不少于![]() 千克,选择哪个采摘园更划算?请说明理由.
千克,选择哪个采摘园更划算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的![]() 型(正方形)、
型(正方形)、![]() 型(菱形)、
型(菱形)、![]() 型(等腰直角三角形)纸片分别放在
型(等腰直角三角形)纸片分别放在![]() 个盒子中,盒子的形状、大小、质地都相同,再将这
个盒子中,盒子的形状、大小、质地都相同,再将这![]() 个盒子装入一只不透明的袋子中.
个盒子装入一只不透明的袋子中.
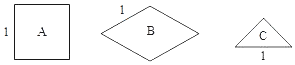
(1)搅匀后从中摸出![]() 个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
个盒子,盒中的纸片既是轴对称图形又是中心对称图形的概率是 ;
(2)搅匀后先从中摸出![]() 个盒子(不放回),再从余下的
个盒子(不放回),再从余下的![]() 个盒子中摸出
个盒子中摸出![]() 个盒子,把摸出的
个盒子,把摸出的![]() 个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
个盒中的纸片长度相等的边拼在一起,求拼成的图形是轴对称图形的概率.(不重叠无缝隙拼接)
查看答案和解析>>
科目:初中数学 来源: 题型:
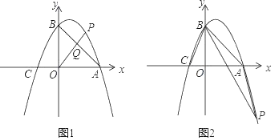
【题目】如图,直线y=﹣x+4与x轴交于点A,与y轴交于点B.抛物线y=﹣![]() x2+bx+c经过A,B两点,与x轴的另外一个交点为C
x2+bx+c经过A,B两点,与x轴的另外一个交点为C
(1)填空:b= ,c= ,点C的坐标为 .
(2)如图1,若点P是第一象限抛物线上的点,连接OP交直线AB于点Q,设点P的横坐标为m.PQ与OQ的比值为y,求y与m的数学关系式,并求出PQ与OQ的比值的最大值.
(3)如图2,若点P是第四象限的抛物线上的一点.连接PB与AP,当∠PBA+∠CBO=45°时.求△PBA的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com