
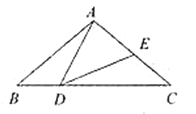
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() ,
,![]() 重合),连接
重合),连接![]() ,
,![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.
(1)当![]() 时,
时,![]() ______
______![]() ,
,![]() ______
______![]() ,点
,点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变______(填“大”或“小”);
逐渐变______(填“大”或“小”);
(2)当![]() 等于多少时,
等于多少时,![]() 与
与![]() 全等?请说明理由.
全等?请说明理由.
【答案】(1)![]() ,
,![]() ,小;(2)
,小;(2)![]() .
.
【解析】
(1)根据三角形内角和定理,将已知数值代入即可求出∠BAD;根据平角求出∠EDC的度数,根据AB=AC可得∠C的度数,根据三角形内角和定理即可求出∠DEC;根据点D的运动方向可判定∠BDA的变化情况.
(2)当DC=2时,利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
解:(1)∠BAD=180°-∠ABD-∠BDA=180°-40°-115°=25°;
∵AB=AC,
∴∠C=∠B=40°
∵∠EDC=180°-∠ADE-∠BDA=180°-40°-115°=25°,
∴∠DEC=180°-∠EDC -∠C=180°-25°-40°=115°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:![]() ,
,![]() ,小;
,小;

(2)当![]() 时,
时,![]() .理由如下:
.理由如下:
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:
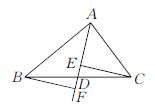
【题目】如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E,F,连结CE,BF.添加一个条件,使得△BDF≌△CDE,你添加的条件是_____________________(不添加辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
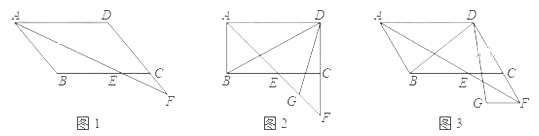
【题目】在平行四边形ABCD中,E是BC上任意一点,延长AE交DC的延长线与点F.
(1)在图中当CE=CF时,求证:AF是∠BAD的平分线.
(2)在(1)的条件下,若∠ABC=90°,G是EF的中点(如图),请求出∠BDG的度数.
(3)如图,在(1)的条件下,若∠BAD=60°,且FG∥CE,FG=CE,连接DB、DG,求出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
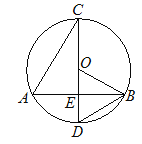
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB.
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
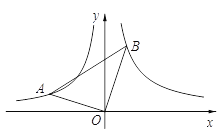
【题目】如图,∠ AOB=90°,且点A,B分别在反比例函数![]() (x<0),
(x<0),![]() (x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
(1)求k1,k2的值;
(2)连接AB,求tan∠ OBA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.
(1)发现:在图1中,![]() ,说明理由;
,说明理由;
(2)探索:如图2,将△ADE绕点A旋转,请求出![]() 的值;
的值;
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DF的中点,若BD⊥CE,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小阳,小杰和小凡到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为10元/千克,下面是他们在活动结束后的对话.
小阳:如果以12元/千克的价格销售,那么每天可售出300千克.
小杰:如果以15元/千克的价格销售,那么每天可获取利润750元.
小凡:我通过调查验证发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获得的利润达600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
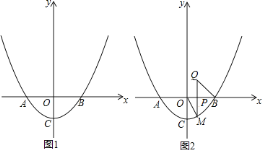
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点
点![]() 是第二象限内一点,过点
是第二象限内一点,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() .求
.求![]() 的值并直接写出
的值并直接写出![]() 的取值范围(利用图
的取值范围(利用图![]() 完成你的探究).
完成你的探究).
![]() 如图
如图![]() ,点
,点![]() 是线段
是线段![]() 上一动点(不包括点
上一动点(不包括点![]() 、
、![]() ),
),![]() 轴交抛物线于点
轴交抛物线于点![]() ,
,![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图),![]() ,
,![]() ,从三角板的刻度可知
,从三角板的刻度可知![]() ,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________
,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为________![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com