
如图,已知![]() .
.
(1)请你在![]() 边上分别取两点
边上分别取两点![]() (
(![]() 的中点除外),连结
的中点除外),连结![]() ,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
,写出使此图中只存在两对面积相等的三角形的相应条件,并表示出面积相等的三角形;
(2)请你根据使(1)成立的相应条件,证明![]() .
.
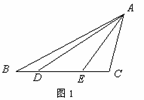
解:(1)如图1,![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)证法一:如图2,分别过点D,B作CA,EA的平行线,两线交于F点,DF与AB交于G点。
所以![]() ,
,![]() 。
。

在![]() 和
和![]() 中,又CE=BD,
中,又CE=BD,
可证![]() 。
。
所以AC=FD,AE=FB。
在![]() 中,AG+DG>AD,
中,AG+DG>AD,
在![]() 中,BG+FG>FB,
中,BG+FG>FB,
所以AG+DG-AD>0,BG+FG-FB>0。
所以AG+DG+BG+FG-AD-FB>0。
即AB+FD>AD+FB。
所以AB+AC>AD+AE。
证法二:如图3,分别过点A,E作CB,CA,的平行线,两线交于F点,EF与AB交于G点,连结BF。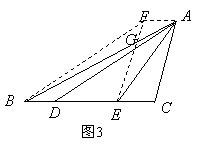
则四边形EFCA是平行四边形。
所以FE=AC,AF=CE。
因为BD=CE,
所以BD=AF。
所以四边形![]() 是平行四边形。
是平行四边形。
所以FB=AD。
在![]() 中,AG+EG>AE,
中,AG+EG>AE,
在![]() 中,BG+FG>FB,
中,BG+FG>FB,
可推得AG+EG+BG+FG>AE+FB。
所以AB+AC>AD+AE。
证法三:如图4,取DE的中点O,连结AO并延长到F点,使得FO=AO,连结EF,CF。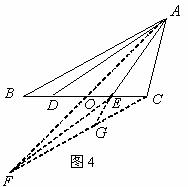
在![]() 和
和![]() 中,又
中,又![]() ,DO=EO。
,DO=EO。
可证![]() 。
。
所以AD=FE。
因为BD=CE,DO=EO,
所以BO=CO。
同理可证![]() 。
。
所以AB=FC。
延长AE交CF于G点。
在![]() 中,AC+CG>AE+EG,
中,AC+CG>AE+EG,
在![]() 中,EG+FG>EF。
中,EG+FG>EF。
可推得AC+CG+EG+FG>AE+EG+EF。
即AC+CF>AE+EF。
所以AB+AC>AD+AE。


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
| 3 |
 =2,∠ADC=30°
=2,∠ADC=30°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com