
如图(1)~(3),已知∠AOB的平分线OM上有一点P,∠CPD的两边与射线OA、OB交于点C、D,连接CD交OP于点G,设∠AOB=α(0°<α<180°),∠CPD=β.
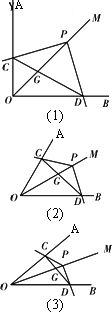
(1)如图(1),当α=β=90°时,试猜想PC与PD,∠PDC与∠AOB的数量关系(不用说明理由);
(2)如图(2),当α=60°,β=120°时,(1)中的两个猜想还成立吗?请说明理由.
(3)如图(3),当α+β=180°时,①你认为(1)中的两个猜想是否仍然成立,若成立请直接写出结论;若不成立,请说明理由.
②若![]() =2,求
=2,求![]() 的值.
的值.
|
(1)PC=PD,∠PDC= (2)成立.理由如下:(3分) 作PE⊥AO于E,PF⊥OB于F,如图.
∵OP平分∠AOB, ∴PE=PF. 在四边形EOFP中, ∵∠AOB=60°,∠PEO=∠PFO=90°, ∴∠EPF=120°,即∠EPC+∠CPF=120°. 又∠CPD=120°,即∠DPF+∠CPF=120°. ∴∠EPC=∠DPF. ∴△EPC≌△FPD. ∴PC=PD.(7分) ∴∠PDC= ∵∠AOB=60°, ∴∠PDC= (3)①成立. ②∵∠PDC= ∠POD= ∴∠PDC=∠POD. 又∠DPG=∠DPO, ∴△PGD∽△PDO. ∴ 又 ∴ |


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=| 4 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com