
【题目】某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示.
销售量p(件) | P=50—x |
销售单价q(元/件) | 当1≤x≤20时,q=30+ 当21≤x≤40时,q=20+ |
(1)求该网店第x天获得的利润y关于x的函数关系式;
(2)这40天中该网店第几天获得的利润最大?最大利润是多少?
【答案】(1)当1≤x≤20时,y=![]() x2+15x+500,当21≤x≤40时,y=
x2+15x+500,当21≤x≤40时,y=![]() 525;(2)这40天中第21天时该网店获得利润最大,最大利润为725元.
525;(2)这40天中第21天时该网店获得利润最大,最大利润为725元.
【解析】
(1)利用利润=售价-成本,分别求出在1≤x≤20和21≤x≤40时,y与x的函数关系式;
(2)当1≤x≤20时,y=-![]() x2+15x+500=-
x2+15x+500=-![]() (x-15)2+612.5,求出一个最大值y1,当21≤x≤40时,求出一个最大值y2,然后比较两者的大小.
(x-15)2+612.5,求出一个最大值y1,当21≤x≤40时,求出一个最大值y2,然后比较两者的大小.
(1)当1≤x≤20时,y=(30+![]() x20)(50x)=
x20)(50x)=![]() x2+15x+500,
x2+15x+500,
当21≤x≤40时,y=(20+![]() 20)(50x)=
20)(50x)=![]() 525;
525;
(2)当1≤x≤20时,y=-![]() x2+15x+500=-
x2+15x+500=-![]() (x-15)2+612.5,
(x-15)2+612.5,
∵![]() <0,
<0,
∴当x=15时,y有最大值y1=612.5,
当21≤x≤40时,
∵26250>0,
∴![]() 随着x的增大而减小,
随着x的增大而减小,
∴x=21时,![]() 最大,
最大,
于是,x=21时,y=![]() 525有最大值y2,且y2=
525有最大值y2,且y2=![]() 525=725,
525=725,
∵y1<y2
∴这40天中第21天时该网店获得利润最大,最大利润为725元.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的正方形放在平面直角坐标系第二象限,使
的正方形放在平面直角坐标系第二象限,使![]() 边落在
边落在![]() 轴负半轴上,且点
轴负半轴上,且点![]() 的坐标是
的坐标是![]() .
.
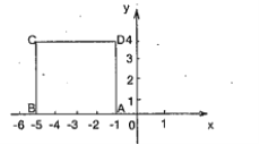
(1)直线![]() 经过点
经过点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若直线![]() 经过点
经过点![]() ,且将正方形
,且将正方形![]() 分成面积相等的两部分,求直线
分成面积相等的两部分,求直线![]() 的解析式;
的解析式;
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行.将(2)中直线
平行.将(2)中直线![]() 沿着
沿着![]() 轴向上平移
轴向上平移![]() 个单位,交
个单位,交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD沿着直线BD折叠,使点C落在C/处,BC/交AD于E,AD=8,AB=4,DE的长=________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=6,AB=10,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE.

(1)求弧DE的长;
(2)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线外一点,连结
为直线外一点,连结![]() .
.
(1)用直尺、圆规在直线![]() 上作点
上作点![]() ,使
,使![]() 为等腰三角形(作出所有符合条件的点
为等腰三角形(作出所有符合条件的点![]() ,保留痕迹).
,保留痕迹).
(2)设![]() ,若(1)中符合条件的点
,若(1)中符合条件的点![]() 只有两点,直接写出
只有两点,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D在AB上,AD=AC,AF⊥CD交CD于点E,交CB于点F,则CF的长是( )
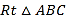
A.1.5B.1.8C.2D.2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() .点
.点![]() 为射线
为射线![]() 上一动点(点
上一动点(点![]() 与
与![]() 不重合),且弦
不重合),且弦![]() 平行于
平行于![]() .
.
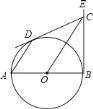
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 设
设![]() 的半径为
的半径为![]() .试问:当动点
.试问:当动点![]() 在射线
在射线![]() 上运动到什么位置时,有
上运动到什么位置时,有![]() ?请回答并证明你的结论.
?请回答并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市投入15000元资金购进![]() 、
、![]() 两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
两种品牌的矿泉水共600箱,矿泉水的成本价和销售价如下表所示:
类别/单价 | 成本价(元/箱) | 销售价(元/箱) |
A品牌 | 20 | 32 |
B品牌 | 35 | 50 |
(1)该大型超市购进![]() 、
、![]() 品牌矿泉水各多少箱?
品牌矿泉水各多少箱?
(2)全部销售完600箱矿泉水,该超市共获得多少利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com