
【题目】已知![]() 、
、![]() 两点在反比例函数
两点在反比例函数![]() 的图象上,下列三个命题:①若
的图象上,下列三个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() ,则
,则![]() ;③过
;③过![]() 、
、![]() 两点的直线与
两点的直线与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,则
,则![]() .其中真命题个数是( )
.其中真命题个数是( )
A.0B.1C.2D.3
【答案】D
【解析】
将点A、B的坐标代入反比例函数解析式中即可判断①;然后利用反比例函数的增减性即可判断②;设![]() ,直线CD的解析式为y=ax+b,然后利用待定系数法求出直线CD的解析式,从而求出点C和点D的坐标,然后根据点A、B的位置分类讨论,分别画出对应的图形,根据三角形的面积公式即可判断③.
,直线CD的解析式为y=ax+b,然后利用待定系数法求出直线CD的解析式,从而求出点C和点D的坐标,然后根据点A、B的位置分类讨论,分别画出对应的图形,根据三角形的面积公式即可判断③.
解:将A、B的坐标代入![]() 中,得
中,得
![]() ,
,![]()
变形可得![]()
若![]()
∴![]() =
=![]() ,故①正确;
,故①正确;
∵![]() >0,x>0
>0,x>0
∴反比例函数图象在第一象限,y随x的增大而减小
∵当![]() <
<![]() ,
,
∴![]() ,故②正确;
,故②正确;
设![]() ,直线CD的解析式为y=ax+b,
,直线CD的解析式为y=ax+b,
∴反比例函数的解析式为![]()
∴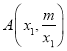 、
、 ,
,
将点A、B的坐标代入y=ax+b中,得
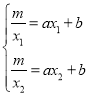
解得: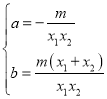
∴直线CD的解析式为![]()
当x=0时,y=![]() ;当y=0时,x=
;当y=0时,x=![]()
∴点D的坐标为(0,![]() ),点C的坐标为(
),点C的坐标为(![]() ,0)
,0)
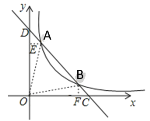
当点B在点A左侧时,过点B作BE⊥y轴于E,过点A作AF⊥x轴于F,如下图所示
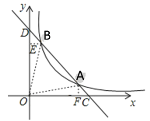
∴AF=![]() ,BE=
,BE=![]() ,OC=
,OC=![]() ,OD=
,OD=![]()
∴S△AOC=![]() OC·AF=
OC·AF=![]()
![]() ·
·![]() =
=![]()
S△BOD=![]() OD·BE=
OD·BE=![]() ·
·![]() ·
·![]() =
=![]()
∴S△AOC= S△BOD;
当点B在点A右侧时,过点A作AE⊥y轴于E,过点B作BF⊥x轴于F,如下图所示
∴BF=![]() ,AE=
,AE=![]() ,OC=
,OC=![]() ,OD=
,OD=![]()
∴S△AOD=![]() OD·AE=
OD·AE=![]() ·
·![]() ·
·![]() =
=![]()
S△BOC=![]() OC·BF=
OC·BF=![]() ·
·![]() ·
·![]() =
=![]()
∴S△AOD= S△BOC
∴S△AOD+S△AOB= S△BOC+S△AOB
∴S△AOC= S△BOD,故③正确.
综上:正确的有结论有3个
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B,DE交AC于点E.
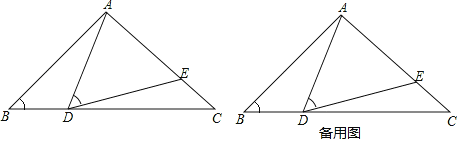
(1)求证:△ABD∽△DCE;
(2)若△DCE为直角三角形,求BD.
(3)若以AE为直径的圆与边BC相切,求AD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱乐器),现将收集到的数据绘制如下的两幅不完整的统计图.
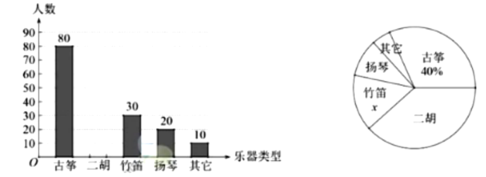
(1)这次共抽取 学生进行调查,扇形统计图中的![]() .
.
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是 度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
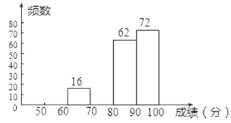
【题目】某校就“遇见路人摔倒后如何处理”的问题,随机抽取该校部分学生进行问卷调查,图1和图2是整理数据后绘制的两幅不完整的统计图. 请根据图中提供的信息,解答下列问题:
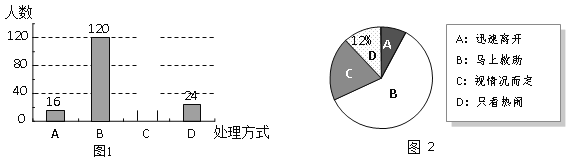
(1)该校随机抽查了 名学生?请将图1补充完整;
(2)在图2中,“视情况而定”部分所占的圆心角是 度;
(3)在这次调查中,甲、乙、丙、丁四名学生都选择“马上救助”,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
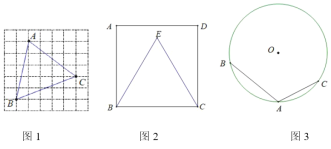
【题目】请仅用无刻度直尺完成下列画图,不写画法,保留画图痕迹.
(1)如图1,在![]() 的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.
的正方形网格中,每个小正方形的边长为1,小正方形的顶点叫做格点.![]() 的顶点在格点上,过点
的顶点在格点上,过点![]() 画一条直线平分
画一条直线平分![]() 的面积;
的面积;
(2)如图2,点![]() 在正方形
在正方形![]() 的内部,且
的内部,且![]() ,过点
,过点![]() 画一条射线平分
画一条射线平分![]() ;
;
(3)如图3,点![]() 、
、![]() 、
、![]() 均在
均在![]() 上,且
上,且![]() ,在优弧
,在优弧![]() 上画
上画![]() 、
、![]() 两点,使
两点,使![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
查看答案和解析>>
科目:初中数学 来源: 题型:
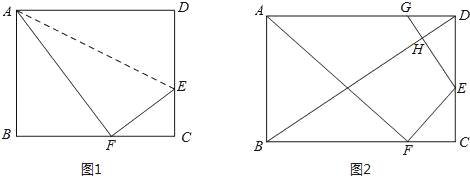
【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处.
(1)如图1,若折痕![]() ,且
,且![]() ,求矩形ABCD的周长;
,求矩形ABCD的周长;
(2)如图2,在AD边上截取DG=CF,连接GE,BD,相交于点H,求证:BD⊥GE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C为⊙O上的定点.连接AB,AC,M为AB上的一个动点,连接CM,将射线MC绕点M顺时针旋转90°,交⊙O于点D,连接BD.若AB=6cm,AC=2cm,记A,M两点间距离为xcm,B,D两点间的距离为ycm.
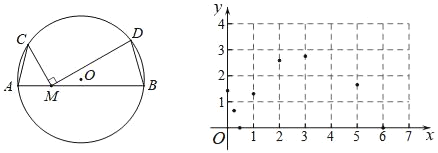
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东探究的过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表,补全表格:
x/cm | 0 | 0.25 | 0.47 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 1.43 | 0.66 | 0 | 1.31 | 2.59 | 2.76 |
| 1.66 | 0 |
(2)在平面直角坐标系xOy中,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BD=AC时,AM的长度约为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com