
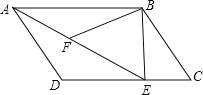
【题目】如图,在平行四边形![]() 中,过点
中,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)求三角形相似就要得出两组对应的角相等,已知了∠BFE=∠C,根据等角的补角相等可得出∠ADE=∠AFB,根据AB∥CD可得出∠BAF=∠AED,这样就构成了两三角形相似的条件.
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.可在直角三角形ABE中用勾股定理求出AE的长,这样就能求出BF的长了.
(1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
∴![]() .
.
∵△ABF∽△EAD,
![]() ,
,
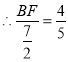 .
.
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
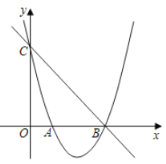
(1)求此抛物线的解析式;
(2)若点![]() 是直线
是直线![]() 下方的抛物线上一动点(不点
下方的抛物线上一动点(不点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
②连接![]() ,
,![]() ,求
,求![]() 的面积最大时点
的面积最大时点![]() 的坐标;
的坐标;
(3)设抛物线的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 是抛物线的对称轴上一点,
是抛物线的对称轴上一点,![]() 为
为![]() 轴上一点,是否存在这样的点
轴上一点,是否存在这样的点![]() 和点
和点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?如果存在,请直接写出点
为顶点的四边形是菱形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
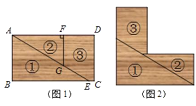
【题目】在综合实践课中,小慧将一张长方形卡纸如图1所示裁剪开,无缝隙不重叠的拼成如图2所示的“![]() ”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知
”形状,且成轴对称图形.裁剪过程中卡纸的消耗忽略不计,若已知![]() ,
,![]() ,
,![]() .
.
求(1)线段![]() 与
与![]() 的差值是___
的差值是___
(2)![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.
S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y=![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2025,n)均在该波浪线上,则![]() =___________.
=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.5m,同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,其中,落在墙壁上的影长为0.8m,落在地面上的影长为4.4m,则树的高为_______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
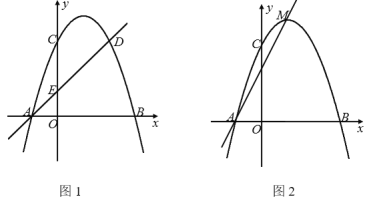
【题目】如图1,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C. 点D(2,3)在该抛物线上,直线AD与y轴相交于点E,点F是直线AD上方的抛物线上的动点.
(1)求该抛物线对应的二次函数关系式;
(2)当点F到直线AD距离最大时,求点F的坐标;
(3)如图2,点M是抛物线的顶点,点P的坐标为(0,n),点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形.①求n的值;②若点T和点Q关于AM所在直线对称,求点T的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
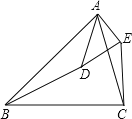
【题目】如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)求证:△ABC∽△ADE;
(2)判断△ABD与△ACE是否相似?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某作物种子发芽率的实验,结果如下表所示:
种子个数 | 200 | 300 | 500 | 700 | 800 | 900 | 1000 |
发芽种子个数 | 187 | 282 | 435 | 624 | 718 | 814 | 901 |
发芽种子率 | 0.935 | 0.940 | 0.870 | 0.891 | 0.898 | 0.904 | 0.901 |
下面有四个推断:
①种子个数是700时,发芽种子的个数是624,所以种子发芽的概率是0.891;
②随着参加实验的种子数量的增加,发芽种子的频率在0.9附近摆动,显示出一定的稳定性,可以估计种子发芽的概率约为0.9(精确到0.1);
③实验的种子个数最多的那次实验得到的发芽种子的频率一定是种子发芽的概率;
④若用频率估计种子发芽的概率约为0.9,则可以估计![]() 种子中大约有
种子中大约有![]() 的种子不能发芽.
的种子不能发芽.
其中合理的是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com