
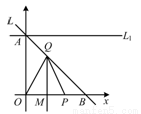
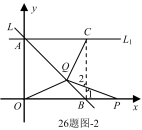
如图,已知直线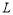 过点
过点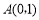 和
和 ,
,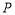 是
是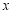 轴正半轴上的动点,
轴正半轴上的动点,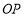 的垂直平分线交
的垂直平分线交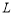 于点
于点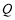 ,交
,交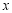 轴于点
轴于点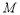 .
.
(1)直接写出直线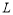 的解析式;
的解析式;
(2)当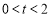 时,设
时,设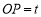 ,
,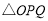 的面积为
的面积为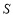 ,求S关于t的函数关系式;并求出S的最大值;
,求S关于t的函数关系式;并求出S的最大值;
(3)当点Q在线段AB上(Q与A、B不重合)时,直线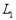 过点A且与x轴平行,问在
过点A且与x轴平行,问在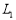 上是否存在点C,使得
上是否存在点C,使得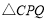 是以
是以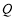 为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
(1)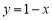 ;
;
(2)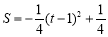 ,当
,当 时,S有最大值
时,S有最大值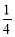 ;
;
(3)在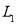 上存在点
上存在点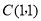 ,使得
,使得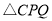 是以
是以 为直角顶点的等腰直角三角形.
为直角顶点的等腰直角三角形.
【解析】
试题分析:(1)已知直线L过A,B两点,可将两点的坐标代入直线的解析式中,用待定系数法求出直线L的解析式;
(2)求三角形OPQ的面积,就需知道底边OP和高QM的长,已知了OP为t,关键是求出QM的长.已知了QM垂直平分OP,那么OM=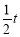 ,
,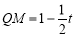 ,再求即可;
,再求即可;
(3)如果存在这样的点C,那么CQ=QP=OQ,因此C,O就关于直线BL对称,因此C的坐标应该是(1,1).那么只需证明CQ⊥PQ即可.分情况进行讨论.
试题解析:(1)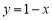 ;
;
(2)∵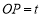 ,∴Q点的横坐标为
,∴Q点的横坐标为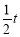 ,
,
当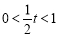 ,即
,即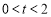 时,
时,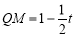 ,
,
∴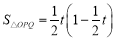 .
.
当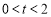 时,
时,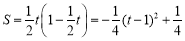 ,
,
∴当 时,S有最大值
时,S有最大值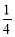 ;
;
(3)∵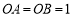 ,∴
,∴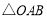 是等腰直角三角形,
是等腰直角三角形,
若在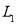 上存在点
上存在点 ,使得
,使得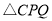 是以
是以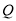 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则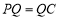 ,
,
∴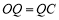 ,∵
,∵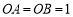 、
、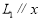 轴,∴
轴,∴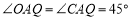
O、C关于直线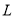 对称∴
对称∴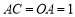 ,得
,得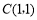 .
.
连接 ,则四边形
,则四边形 是正方形.
是正方形.
(i)当点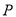 在线段
在线段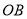 上,如图–1.
上,如图–1.

由对称性,得
 ,
,
∴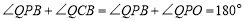 ,
,
∴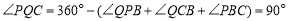 .
.
即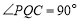
(ii)当点 在线段
在线段 的延长线上,如图–2,
的延长线上,如图–2,
∵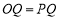 ∴
∴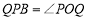 由对称性可知
由对称性可知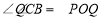
∴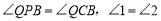 ,
,
∴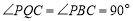 .
.
综合(i)(ii),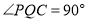 .
.
∴在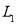 上存在点
上存在点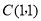 ,使得
,使得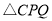 是以
是以 为直角顶点的等腰直角三角形.
为直角顶点的等腰直角三角形.
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
已知:如图, AB是⊙O的直径,AM和BN是⊙O的两条切线,点D是AM上一点,联结OD , 作BE∥OD交⊙O于点E, 联结DE并延长交BN于点C.
(1)求证:DC是⊙O的切线;
(2)若AD=l,BC=4,求直径AB的长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市丰台区中考二模数学卷(解析版) 题型:选择题
某班第一小组6名女生在测仰卧起坐时,记录下她们的成绩(单位:个/分):45,48,46,50,50,49.这组数据的平均数是( )
A.49 B.48 C.47 D.46
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古满洲里市九年级三月月考数学试卷(解析版) 题型:填空题
某同学的身高为1.4米,某一时刻他在阳光下的影长为1.2米,此时,与他相邻的一棵小树的影长为3.6米,则这棵树的高度为 米.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古满洲里市九年级三月月考数学试卷(解析版) 题型:选择题
为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比 ( )
A. 保持不变 B. 减少9m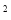 C. 增加6m
C. 增加6m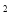 D. 增加9m
D. 增加9m
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古九年级6月中考模拟数学试卷(解析版) 题型:解答题
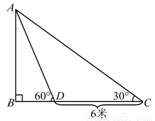
某中学九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆顶端A的仰角为30°,向前走了6米到达D点,在D点测得旗杆顶端A的仰角为60°(测角器的高度不计).
(1)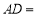 米;
米;
(2)求旗杆AB的高度(结果保留1位小数,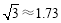 ).
).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古呼伦贝尔市九年级第四次月考数学试卷(解析版) 题型:解答题
已知二次函数的图象经过点(0,- 3),且顶点坐标为(1,- 4).求这个解析式。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com