
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,过点
的中点,过点![]() 的直线分别与
的直线分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
【答案】B
【解析】
连接BD,先证明△BOC是等边三角形,得出BO=BC,又FO=FC,从而可得出FB⊥OC,故①正确;因为△EOB≌△FOB≌△FCB,故△EOB不会全等于△CBM,故②错误;再证明四边形EBFD是平行四边形,由OB⊥EF推出四边形EBFD是菱形,故③正确;先在Rt△BCF中,可求出BC的长,再在Rt△BCM中求出BM的长,从而可知④错误,最后可得到答案.
解:连接BD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,∴BD也过O点,
∴OB=OC,
∵∠COB=60°,
∴△OBC是等边三角形,∴OB=BC,
又FO=FC,BF=BF,
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,∴①正确;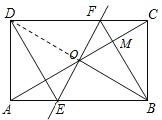
∵∠OBC=60°,∴∠ABO=30°,
∵△OBF≌△CBF,∴∠OBM=∠CBM=30°,∴∠ABO=∠OBF,
∵AB∥CD,∴∠OCF=∠OAE,
∵OA=OC,易证△AOE≌△COF,∴OE=OF,
∵OB=OD,
∴四边形EBFD是平行四边形.
又∠EBO=∠OBF,OE=OF,
∴OB⊥EF,∴四边形EBFD是菱形,
∴③正确;
∵由①②知△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误,
∴②错误;
∵FC=2,∠OBC=60°,∠OBF=∠CBF,
∴∠CBF=30°,∴BF=2CF=4,∴BC=2![]() ,
,
∴CM=![]() BC=
BC=![]() ,∴BM=3,故④错误.
,∴BM=3,故④错误.
综上可知其中正确结论的个数是2个.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,点![]() 在第一象限,
在第一象限,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() ,且四边形
,且四边形![]() 的面积为48.
的面积为48.

(1)如图1,直接写出点A、B、O、C的坐标:
(2)如图2,点![]() 从
从![]() 出发以每秒1个单位的速度沿
出发以每秒1个单位的速度沿![]() 轴正半轴运动,同时点
轴正半轴运动,同时点![]() 从B出发,以每秒2个单位的速度沿射线
从B出发,以每秒2个单位的速度沿射线![]() 运动,
运动,![]() 交线段
交线段![]() 于
于![]() ,设运动的时间为
,设运动的时间为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)如图3,将线段![]() 平移,使点
平移,使点![]() 的对应点恰好落在
的对应点恰好落在![]() 轴负半轴上,点
轴负半轴上,点![]() 的对应点为
的对应点为![]() ,连
,连![]() 交
交![]() 轴交于
轴交于![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标。
的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢球后,足球踢到了小华处的概率是多少(用树状图或列表的方法加以说明)?
(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() 分)在菱形
分)在菱形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点.
上的一个动点.
(![]() )如图①,求
)如图①,求![]() 的最小值.
的最小值.
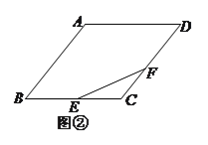
(![]() )如图②,若
)如图②,若![]() 也是
也是![]() 边上的一个动点,且
边上的一个动点,且![]() ,求
,求![]() 的最小值.
的最小值.
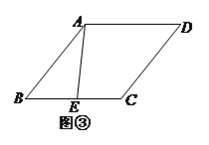
(![]() )如图③,若
)如图③,若![]() ,则在菱形内部存在一点
,则在菱形内部存在一点![]() ,使得点
,使得点![]() 分别到点
分别到点![]() 、点
、点![]() 、边
、边![]() 的距离之和最小.请你画出这样的点
的距离之和最小.请你画出这样的点![]() ,并求出这个最小值.
,并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个长方形的边长如图所示(![]() 为正整数),其面积分别为
为正整数),其面积分别为![]() .
.
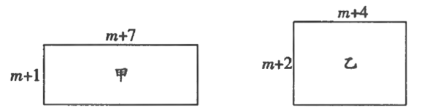
(1)填空:![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)若一个正方形的周长等于甲、乙两个长方形的周长之和.
①设该正方形的边长为![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示);
的代数式表示);
②设该正方形的面积为![]() ,试探究:
,试探究: ![]() 与
与![]() 的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由,
的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由,
(3)若另一个正方形的边长为正整数![]() ,并且满足条件
,并且满足条件![]() 的
的![]() 有且只有4个,求
有且只有4个,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC=8,BO=![]() AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.
AB,点M为BC边上一动点,将线段OM绕点O按逆时针方向旋转90°至ON,连接AN、CN,则△CAN周长的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
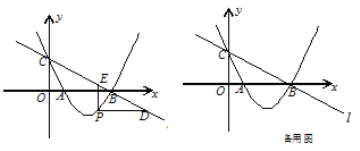
【题目】如图,直线![]() :
: ![]() 与
与![]() 轴、
轴、![]() 轴分别交于点B、C,经过B、C两点的抛物线
轴分别交于点B、C,经过B、C两点的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求该抛物线的解析式;
(2)若点P在直线![]() 下方的抛物线上,过点P作PD∥
下方的抛物线上,过点P作PD∥![]() 轴交
轴交![]() 于点D,PE∥
于点D,PE∥![]() 轴交
轴交![]() 于点E,
于点E,
求PD+PE的最大值;
(3)设F为直线![]() 上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
上的点,以A、B、P、F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
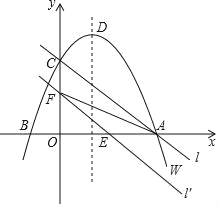
如图,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣x2+2x+3,抛物线W与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,它的顶点为D,直线l经过A、C两点.
(1)求点A、B、C、D的坐标.
(2)将直线l向下平移m个单位,对应的直线为l′.
①若直线l′与x轴的正半轴交于点E,与y轴的正半轴交于点F,△AEF的面积为S,求S关于m的函数关系式,并写出自变量m的取值范围;
②求m的值为多少时,S的值最大?最大值为多少?
(3)若将抛物线W也向下平移m单位,再向右平移1个单位,使平移后得到的二次函数图象的顶点P落在△AOC的内部(不包括△AOC的边界),请直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com