
【题目】抛物线M:y=ax2-4ax+a-1(a≠0)与x轴交于A,B两点(点A在点B左侧),抛物线的顶点为D.
(1)抛物线M的对称轴是直线______;
(2)当AB=2时,求抛物线M的函数表达式;
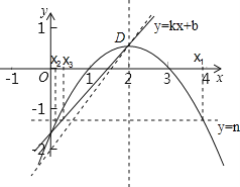
(3)在(2)的条件下,直线l:y=kx+b(k≠0)经过抛物线的顶点D,直线y=n与抛物线M有两个公共点,它们的横坐标分别记为x1,x2,直线y=n与直线l的交点的横坐标记为x3(x3>0),若当-2≤n≤-1时,总有x1-x3>x3-x2>0,请结合函数的图象,直接写出k的取值范围.
【答案】(1)x=2;(2)y=-![]() x2+2x-
x2+2x-![]() ;(3)k>
;(3)k>![]()
【解析】
(1)根据抛物线解析式,即可得出其对称轴所在直线;
(2)根据抛物线的对称轴得出A、B两点坐标,代入抛物线解析式求解,即可得出其解析式;
(3)首先将抛物线化为顶点式,得出点D坐标,然后根据直线与抛物线的交点坐标结合函数图象,即可判定k的取值范围.
(1)∵抛物线M的表达式为y=ax2-4ax+a-1,
∴抛物线M的对称轴为直线x=-![]() =2.
=2.
故答案为:x=2.
(2)∵抛物线y=ax2-4ax+a-1的对称轴为直线x=2,抛物线M与x轴的交点为点A、B(点A在点B左侧),AB=2,
∴点A的坐标为(1,0),点B的坐标为(3,0).
将A(1,0)代入y=ax2-4ax+a-1,得:a-4a+a-1=0,
解得:a=-![]() ,
,
∴抛物线M的函数表达式为y=-![]() x2+2x-
x2+2x-![]() .
.
(3)∵y=-![]() x2+2x-
x2+2x-![]() =-
=-![]() (x-2)2+
(x-2)2+![]() ,
,
∴点D的坐标为(2,![]() ).
).
∵直线y=n与直线l的交点的横坐标记为x3(x3>0),且当-2≤n≤-1时,总有x1-x3>x3-x2>0,
∴直线l与y轴的交点在(0,-2)下方,
∴b<-2.
∵直线l:y=kx+b(k≠0)经过抛物线的顶点D,
∴2k+b=![]() ,
,
∴k=![]() -
-![]() >
>![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
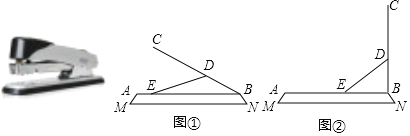
【题目】在日常生活中我们经常会使用到订书机,如图MN是装订机的底座,AB是装订机的托板AB始终与底座平行,连接杆DE的D点固定,点E从A向B处滑动,压柄BC绕着转轴B旋转.已知连接杆BC的长度为20cm,BD=![]() cm,压柄与托板的长度相等.
cm,压柄与托板的长度相等.
(1)当托板与压柄的夹角∠ABC=30°时,如图①点E从A点滑动了2cm,求连接杆DE的长度.
(2)当压柄BC从(1)中的位置旋转到与底座垂直,如图②.求这个过程中,点E滑动的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 的环湖越野赛中,甲乙两选手的行程
的环湖越野赛中,甲乙两选手的行程![]() (单位:
(单位:![]() )随时间
)随时间![]() (单位:
(单位:![]() )变化的图象如图所示,根据图中提供的信息,下列说法中,错误的是:( )
)变化的图象如图所示,根据图中提供的信息,下列说法中,错误的是:( )
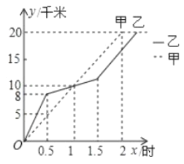
A.出发后1小时,两人行程均为![]() ;B.出发后1.5小时,甲的行程比乙多
;B.出发后1.5小时,甲的行程比乙多![]() ;
;
C.两人相遇前,甲的速度小于乙的速度;D.甲比乙先到达终点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)若∠FDB=30°,∠ABC=45°,BC=4![]() ,求DF的长.
,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点出发,分别沿
两点出发,分别沿![]() 、
、![]() 方向匀速移动,它们的移动速度都是
方向匀速移动,它们的移动速度都是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 、
、![]() 两点停止运动,设点
两点停止运动,设点![]() 的运动时间的
的运动时间的![]() 秒,解答下列问题.
秒,解答下列问题.
(1)![]() 时,求
时,求![]() 的面积;
的面积;
(2)若![]() 是直角三角形,求
是直角三角形,求![]() 的值;
的值;
(3)用![]() 表示
表示![]() 的面积并判断
的面积并判断![]() 能否成立,若能成立,求
能否成立,若能成立,求![]() 的值,若不能成立,说明理由.
的值,若不能成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏省第十九届运动会将于2018年9月在扬州举行开幕式,某校为了了解学生“最喜爱的省运会项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的省运会项目的人数调查统计表


根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 ,![]() ;
;
(2)扇形统计图中“自行车”对应的扇形的圆心角为 度;
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
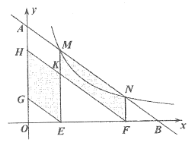
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() 、
、![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() ,
,![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 和四边形
和四边形![]() 的面积和为12,则
的面积和为12,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com