Question

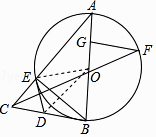
【题目】如图，△ABE是⊙O的内接三角形，AB为直径，过点B的切线与AE的延长线交于点C，D是BC的中点，连接DE，连接CO，线段CO的延长线交⊙O于F，FG⊥AB于G．
（1）求证：DE是⊙O的切线；
（2）若AE=4，BE=2，求AG的长．

Answer 1

【答案】
（1）证明：连接OE，OD，

在△OED与△OBD中， ，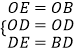

∴△OED≌△OBD，

∴∠OED=∠OBD，

∵BC是⊙O的切线，

∴∠OBD=90°，

∴∠OED=90°，

∴OE⊥ED，

∴DE是⊙O的切线；

（2）解：∵AB为⊙O的直径，

∴∠AEB=90°，

∴AB= =2 ，

∴OF=OB= ，

∵△AEB∽△BEC，

∴ ，

∴BC= = ，

∴OC= = = ，

∵∠AOF=∠BOC，

∵FG⊥AB，

∴∠FGO=90°，

∴∠FGO=∠OBC=90°，

∴△OFG∽△OBC，

∴ ，

∴OG= OB= ，

∴AG=AO﹣OG= ﹣ ．

【解析】（1）连接OE，OD，根据全等三角形的性质得到∠OED=∠OBD，由BC是⊙O的切线，得到∠OBD=90°，于是得到结论；（2）由AB为⊙O的直径，得到∠AEB=90°，根据勾股定理得到AB= =2 ，求得OF=OB= 根据相似三角形的性质得到BC= = ，根据勾股定理到OC= = = ，根据相似三角形的性质即可得到结论．