练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

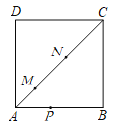
    【题目】如图，在正方形ABCD中，M、N是对角线AC上的两个动点，P是正方形四边上的任意一点，且，．关于下列结论：①当△PAN是等腰三角形时，P点有6个；②当△PMN是等边三角形时，P点有4个；③DM+DN的最小值等于6．其中，一定正确的结论的序号是_______．

    【答案】①②③

    【解析】

    ①②利用图象法即可解决问题.③连接DB，与AC相交于点O，利用正方形的性质求出相应线段的长，并根据二次函数的性质即可得解.

    ①如图，△PAN是等腰三角形时，P点有6个；故正确；

    ②如图2，当△PMN是等边三角形时，P点有4个；故正确；

    ③连接DB，与AC相交于点O，如图，

    ∵四边形ABCD是正方形，且AB=4；

    设，则

    即

    时，DM=DN=3最小

    即的最小值为6，故③正确

    故答案为：①②③．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明手中有4张背面相同的扑克牌：红桃6、红桃9、黑桃6、黑桃9．先将4张牌背面朝上洗匀，再让小丽抽牌．

    （1）小丽从中任意抽取一张扑克牌，抽到黑桃9的概率是__________，抽到偶数的概率是_________；

    （2）小丽从中任意抽取两张扑克牌，游戏规则规定：若小丽抽到的两张牌是一红一黑，则小丽胜，若小丽抽到的两张牌是一奇一偶，则小明胜，问该游戏对双方是否公平．（利用树状图或列表说明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数与轴交于、两点，，与直线交于、两点，点在轴上，．

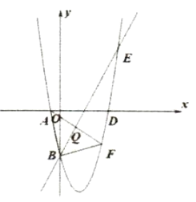
    （1）求二次函数的解析式；

    （2）在抛物线上有一点，若的面积为，求点的横坐标；

    （3）点在第四象限的抛物线上运动，连接，与直线交于点，连接，．设的面积为，的面积为，求的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

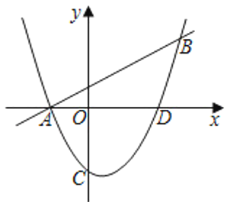
    【题目】如图，一次函数y＝x+1的图象与二次函数y＝x2+bx+c的图象交于A，B两点，点A在x轴上．点B的横坐标为4．

    （1）b＝　 　，c＝　 　；

    （2）设二次函数的图象与y轴交于C点，与x轴的另一个交点为D．连接AC，CD，求∠ACD的正弦值；

    （3）若M点在x轴下方二次函数图象上，

    ①过M点作y轴平行线交直线AB于点E，以M点为圆心，ME的长为半径画圆，求圆M在直线AB上截得的弦长的最大值；

    ②若∠ABM＝∠ACO，则点M的坐标为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

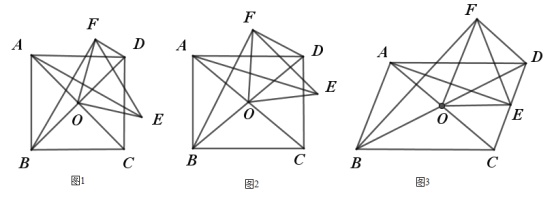
    【题目】如图1，正方形ABCD的对角线AC，BD交于点O，将△COD绕点O逆时针旋转得到△EOF（旋转角为锐角），连AE，BF，DF，则AE=BF．

    （1）如图2，若（1）中的正方形为矩形，其他条件不变．

    ①探究AE与BF的数量关系，并证明你的结论；

    ②若BD=7，AE=，求DF的长；

    （2）如图3，若（1）中的正方形为平行四边形，其他条件不变，且BD=10，AC=6，AE=5，请直接写出DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着《流浪地球》的热播，其同名科幻小说的销量也急剧上升．为应对这种变化，某网店分别花20000元和30000元先后两次增购该小说，第二次的数量比第一次多500套，且两次进价相同．

    （1）该科幻小说第一次购进多少套？

    （2）根据以往经验：当销售单价是25元时，每天的销售量是250套；销售单价每上涨1元，每天的销售量就减少10套．网店要求每套书的利润不低于10元且不高于18元．

    ①直接写出网店销售该科幻小说每天的销售量y（套）与销售单价x（元）之间的函数关系式及自变量x的取值范围；

    ②网店决定每销售1套该科幻小说，就捐赠a（0＜a＜7）元给困难职工，每天扣除捐赠后可获得的最大利润为1960元，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

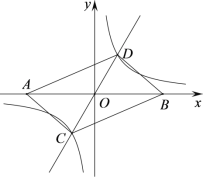
    【题目】如图，在平面直角坐标系中，点A的坐标为(m，0)，m＜0，点B与点A 关于原点对称，直线与双曲线交于C，D两点．

    (1)直接判断后填空：四边形ACBD的形状一定是 ；

    (2)若点D(1，t)，求双曲线的解析式；

    (3)在(2)的前提下，四边形ACBD为矩形时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有甲乙两个玩具小汽车在笔直的240米跑道上进行折返跑游戏，甲从点出发，匀速在、之间折返跑，同时乙从点出发，以大于甲的速度匀速在、之间折返跑．在折返点的时间忽略不计．

    （1）若甲的速度为，乙的速度为，第一次迎面相遇的时间为，则与的关系式___________；

    （注释：当两车相向而行时相遇是迎面相遇，当两车在点相遇时也视为迎面相遇）

    （2）如图1，

    ①若甲乙两车在距点20米处第一次迎面相遇，则他们在距点_______米第二次迎面相遇：

    ②若甲乙两车在距点50米处第一次迎面相遇，则他们在距点__________米第二次迎面相遇；

    （3）设甲乙两车在距点米处第一次迎面相遇，在距点米处第二次迎面相遇．某同学发现了与的函数关系，并画出了部分函数图象（线段，不包括点，如图2所示）．

    ①则_______，并在图2中补全与的函数图象（在图中注明关键点的数据）；

    ②分别求出各部分图象对应的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A在反比例函数(x<0)的图象上，连接OA，分别以点O和点A为圆心，大于的长为半径作弧，两弧相交于B，C两点，过B，C两点作直线交x轴于点D，连接AD．若∠AOD＝30°，△AOD的面积为2，则k的值为（　　）

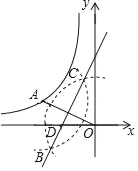
    A.﹣6B.6C.﹣2D.﹣3

    查看答案和解析>>

    同步练习册答案